Tập A = 52 , 54 , 56 , 58 là tập các số chia hết cho 2. Vậy tập A được lập từ các chữ số nào?
A. 5; 2; 4; 6
B. 5; 2; 4; 8
C. 5; 5; 5; 2; 4; 6; 8
D. 5; 2; 4; 6; 8
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi \(S=\left\{\overline{abc}\right\}\)
a có 5 cách chọn
b có 5 cách chọn
c có 4 cách chọn
=>S có 5*5*4=100 số
Gọi \(\overline{abc}\) là số chia hết cho 5
TH1: c=5
=>a có 4 cách và b có 4 cách
=>Có 16 cách
TH2: c=0
=>a có 5 cách và b có 4 cách
=>Có 5+4=20 cách
=>Có 16+20=36(cách)
\(n\left(\Omega\right)=C^2_{100}\)
\(n\left(B\right)=C^2_{36}\)
=>\(P\left(B\right)=\dfrac{7}{55}\)

Tập S có 9 4 phần tử. Ta có
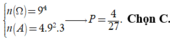
Thật vậy: Gọi số thỏa mãn biến cố là ![]()
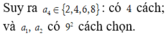
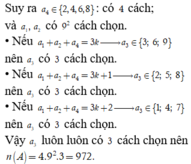

Chọn A
Số phần tử của A là A 9 4 = 3024 số.
Số phần tử của không gian mẫu là n ( Ω ) = 3024
Gọi A là biến cố: “Chọn được một số chia hết cho 11 và tổng bốn chữ số của nó chia hết cho 11”.
Xét số tự nhiên có 4 chữ số có dạng ![]()
Theo bài ra ta có: ![]() và
và ![]()
Suy ra ![]()
Trong các chữ số 1;2;3;4;5;6;7;8;9 có các bộ số mà tổng chia hết cho 11 là ![]()
Chọn 2 cặp trong 4 cặp số trên để tạo số ![]()
Chọn {a;c} có 4 cách, chọn {b;d} có 3 cách, sau đó sắp thứ tự các số a, b, c, d. Ta được 4.3.2.2 = 48
Suy ra n(A) = 48
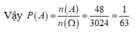

Gọi số đó là \(\overline{abc}\)
Không gian mẫu: \(6.6.5=180\)
a. TH1: \(c=0\Rightarrow ab\) có \(A_6^2\) cách
TH2: \(c\ne0\Rightarrow c\) có 3 cách chọn, ab có \(5.5=25\) cách
Xác suất: \(P=\dfrac{3.25+A_6^2}{180}=\)
b. Tổng 3 chữ số chia hết cho 3 khi 3 số đồng dư khi chia 3 hoặc 3 số đôi một khác số dư khi chia 3.
- 3 số đồng dư khi chia cho 3: \(3!-2!=4\) số
- 3 số chia 3 có 3 số dư khác nhau:
+ Không có mặt số 0: \(C_2^1C_2^1C_2^1.3!=48\)
+ Có mặt số 0: \(C_2^1C_2^1C_2^1\left(3!-2!\right)=32\)
Xác suất: \(P=\dfrac{4+48+32}{180}=...\)
Đáp án D
52; 54; 56; 58 được lập từ các chữ số 5; 2; 4; 6; 8