Chia 48 thành bốn phần tỉ lệ với các số là 3; 5; 7; 9. Các số đó theo thứ tự tăng dần là?
A. 6; 12; 14; 18
B. 18; 14; 10; 6
C. 6; 14; 10; 18
D. 6; 10; 14; 18
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

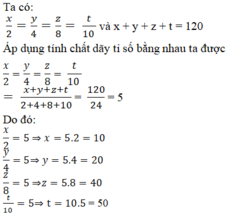
Vậy các số cần tìm sắp xếp theo thứ tự tăng dần là 10; 20; 40; 50
Đáp án cần chọn là: D

\(\text{Mỗi phần là: }48:\left(3+5+7+9\right)=2\)
\(\Rightarrow\text{4 số cần chia là: }6;10;14;18\)
Gọi 4 phần cần chia là : a,b,c,d
Theo đề bài ta có:
\(\frac{a}{3}=\frac{b}{5}=\frac{c}{7}=\frac{d}{9}\) và\(a+b+c+d=48\)
\(\Rightarrow\frac{a+b+c+d}{3+5+7+9}=\frac{48}{24}=2\)
\(\frac{a}{3}=2\Leftrightarrow a=2.3=6\)
\(\frac{b}{5}=2\Leftrightarrow a=2.5=10\)
\(\frac{c}{7}=2\Leftrightarrow a=2.7=14\)
\(\frac{d}{9}=2\Leftrightarrow2.9=18\)
Vậy 4 phần cần chia lần lượt là : 6,10,14,18.

a) gọi ba số a,b,c
theo dãy số dằng nhau ta có \(\frac{a}{2}\)=\(\frac{b}{3}\)=\(\frac{c}{4}\)=>\(\frac{a+b+c}{2+3+4}\)=\(\frac{99}{9}\)=11
=> a=22. b=33,c=44
b) tương tự gọi 3 số a,b,c,
theo dãy số dằng nhau ta có \(\frac{a}{3}\)=\(\frac{b}{3}\)=\(\frac{c}{4}\)=>\(\frac{a+b+c}{3+5+7}\)=\(\frac{285}{3+5+7}\)=19
=> a=57,b=95, c=133
c) tương tự bốn số là:\(\frac{247}{4}\);\(\frac{2717}{28}\);\(\frac{3211}{28}\);\(\frac{6175}{28}\)
d, tương tự : bốn số là 60; 105;120;180

X và Y và Z tỉ lệ thuận với 3;4 và 5
Ta có: x/3 = y/4 = z/5
= x - y + z / 3+4+5=20/12
x/3 = 20/12 => x

Câu hỏi của Phạm Minh Phương t - Toán lớp 7 - Học toán với OnlineMath
Câu 1:
Gọi ba phần được chia từ số 470 lần lượt là x, y, z
Có: Ba phần tỉ lệ nghịch với 3, 4, 5
⇒x3=y4=z5⇒x20=y15=z12⇒x3=y4=z5⇒x20=y15=z12 và x+y+z=470x+y+z=470
Áp dụng tính chất dãy tỉ số bằng nhau
x20=y15=z12=x+y+z20+15+12=47047=10x20=y15=z12=x+y+z20+15+12=47047=10
⇒\hept⎧⎨⎩x=200y=150z=120

Gọi bốn số cần tìm là a,b,c,d
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{a}{\dfrac{1}{2}}=\dfrac{b}{\dfrac{1}{5}}=\dfrac{c}{\dfrac{1}{7}}=\dfrac{d}{\dfrac{1}{14}}=\dfrac{a+b+c+d}{\dfrac{1}{2}+\dfrac{1}{5}+\dfrac{1}{7}+\dfrac{1}{14}}=\dfrac{128}{\dfrac{32}{35}}=140\)
Do đó: a=70; b=28; c=20; d=10

gọi 4 phần cần tìm là x, y, z, t
Ta có:
\(\frac{x}{y}=\frac{2}{3}=\frac{16}{24}\)=>\(\frac{x}{16}=\frac{y}{24}\)
\(\frac{y}{z}=\frac{4}{5}=\frac{24}{30}\)=>\(\frac{y}{24}=\frac{z}{30}\)
\(\frac{z}{t}=\frac{6}{7}=\frac{30}{35}\)=>\(\frac{z}{30}=\frac{t}{35}\)
áp dụng t/c của dãy tỉ số bằng nhau ta có
\(\frac{x}{16}=\frac{y}{24}=\frac{z}{30}=\frac{t}{35}=\frac{x+z+y+t}{16+24+30+35}=\frac{210}{105}=2\)
do đó:
\(\frac{x}{16}=2\)=>\(x=32\)
\(\frac{z}{30}=2\)=>\(z=60\)
\(\frac{y}{24}=2\)=>\(y=48\)
\(\frac{t}{35}=2\)=>\(t=70\)
vậy phần thứ 1 là 32, phần thứ 2 là 60, phần thứ 3 là 48 và thần nhứ 4 có 70
Giả sử 48 chia thành bốn phần là x; y; z; t tỉ lệ với các số 3; 5; 7; 9
Ta có: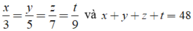
Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:
Do đó: x = 6; y = 10; z = 14; t = 18
Chọn đáp án D.