Cho tam giác vuông cân ABC với A B = A C = a . Khi quay tam giác đó (cùng với phần trong của nó) quanh đường thẳng đi qua B và song song với AC, ta được khối tròn có thể tích bằng
A. 2 πa 3 3
B. 2 πa 3 5
C. πa 3 3
D. πa 3 2
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn A
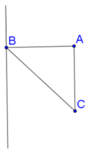
Thể tích khối tròn thu được bằng hiệu thể tích hình trụ bán kính đáy AB chiều cao AC trừ cho thể tích nón đỉnh B bán kính đáy AB chiều cao AC
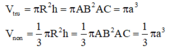

Đáp án A
Công thức thể tích khối nón V n o n = 1 3 π R 2 h ;
Ở đây R = O C .
Ta có 1 O C 2 = 1 C A 2 + 1 C B 2 = 1 a 2 + 1 b 2 = a 2 + b 2 a 2 b 2 ⇒ O C = a b a 2 + b 2 = R
Thể tích khối tròn xoay cần tính
V = 1 3 π O C 2 . O B + 1 3 π O C 2 . O A = 1 3 π R 2 . A B = 1 3 π a 2 b 2 a 2 + b 2 . a 2 + b 2 = π 3 . a 2 b 2 a 2 + b 2

Chọn C.
Phương pháp:
Dựng hình, xác định các hình tròn xoay tạo thành khi quay và tính tỉ số thể tích.
Cách giải:
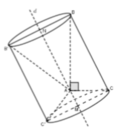
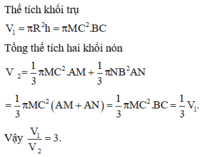

Thể tích của hình tròn xoay được tạo ra bằng thể tích của hình trụ có \(R=h=a\) trừ thể tích hình nón có \(R=a;h=a;l=a\sqrt{2}\)
\(\Rightarrow V=\pi.R^2h-\frac{1}{3}\pi R^2h=\frac{2}{3}\pi R^2h=\frac{2}{3}\pi a^3\)

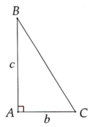
a, S x q N 1 = πAC . BC = π . b . b 2 + c 2 = S 1
S x q N 2 = πA B . BC = π . c . b 2 + c 2 = S 2
=> S 1 ≠ S 2
b, V N 1 = 1 3 π . AC 2 . AB = 1 3 b 2 c
V N 2 = 1 3 π . A B 2 . A C = 1 3 c 2 b
=> V N 1 ≠ V N 2

a: Xét tứ giác AEDF có
AE//DF
AF//DE
AD là phân giác của góc FAE
Do đó: AEDF là hình thoi
b: Xét ΔAMD vuông tại M và ΔAND vuông tại N có
AD chung
góc MAD=góc NAD
Do đó; ΔAMD=ΔAND
=>AM=AN
Xét ΔAEF có AM/AF=AN/AE
nên MN//EF
Đáp án A
Thể tích khối tròn thu được bằng hiệu thể tích hình trụ bán kính đáy AB chiều cao AC trừ cho thể tích nón đỉnh B bán kính đáy AB chiều cao AC