Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Vì vai trò của m,n như nhau nên với mỗi n sẽ có 1 m tương ứng
Vậy có tất cả 4 bộ số thỏa mãn yêu cầu bài toán Chọn B
Đáp án C
Gọi 
là 4 đường thẳng song song với BC.
Gọi 
là 5 đường thẳng song song với AC.
Gọi 
là 6 đường thẳng song song với AB.
Cứ 2 đường thẳng song song và hai đường thẳng không song song tạo thành một hình thang.
Vậy số hình thành là
Số cách chọn 2 đường thằng song song trong 6 đường thằng song song là: \(C_6^2\) (cách chọn)
Số cách chọn 2 đường thằng song song trong 8 đường thằng song song cùng vuông góc với 6 đường thằng song song ban đầu là: \(C_8^2\) (cách chọn)
Áp dụng quy tắc nhân, ta có số hình chữ nhật có thể tạo thành là: \(C_8^2.C_6^2 = 420\) ( hình chữ nhật)
Đáp án C
2. Nếu 3 mặt phẳng đôi một cắt nhau theo 3 giao tuyến phân biệt thì 3 giao tuyến ấy hoặc đồng quy, hoặc đôi một song song với nhau
8. Cho 2 đường thẳng chéo nhau. Có duy nhất một mặt phẳng chứa đường thẳng này và song song với đường thẳng kia
Việc lập một hình chữ nhật được thực hiện bởi hai bước:
+ Chọn 2 đường thẳng trong số 4 đường thẳng.
Có: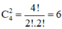 
cách chọn.
+ Chọn 2 đường thẳng trong số 5 đường thẳng vuông góc
Có: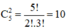 
cách chọn.
⇒ Theo quy tắc nhân: Có 10.6 = 60 (cách lập hình chữ nhật).
Đáp án C
Mệnh đề 1 đúng.
Mệnh đề 2 sai vì 2 đường thẳng đó có thể chéo nhau.
Mệnh đề 3 sai vì 2 đường thẳng đó có thể song song.
Mệnh đề 4 sai
Chọn D