cho đoạn thẳng AB va trung điểm M của nó.Chứng tỏ
rằng nếu C là điểm nằm giữa M và B thì
CM=CA-CB chia 2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
8 tháng 12 2017
Vì M là t/đ của AB => MA = MB = \(\frac{AB}{2}\)
Nếu C n/g M và B
=> CM+ CB = MB
=> CM = MB - CB
Hay CM = AB / 2 - CB (1)
Vì C n/g A và B => AC + BC = AB (2)
Từ (1) và (2) => CM = AC + BC / 2 - CB
CM = AC + BC /2 - 2CB / 2
CM = \(\frac{\left(AC+BC-2CB\right)}{2}\)
CM = \(\frac{CA-CB}{2}\)
Vậy .....
CM
7 tháng 11 2018
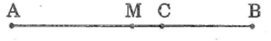
Vì M là trung điểm AB nên AM = MB
Vì M nằm giữa A và C nên AM + MC = AC
Vì C nằm giữa B và M nên BC + MC = BM ⇒ BC = BM – MC
Suy ra: AC > BC
Ta có: AC – BC = (AM + MC) – (BM – MC )
= AM + MC – BM + MC = 2MC
⇒ CM = (CA-CB)/2
14 tháng 5 2017
M là trung điểm AB => MA = MB => AB=2MB
Có: \(CM=CB+MB=\frac{2CB+2MB}{2}=\frac{2CB+AB}{2}=\frac{CB+\left(AB+CB\right)}{2}=\frac{CB+CA}{2}\)
31 tháng 1 2016
a, ta có:
CA=AM cộng CM vì M nằm giữa A và C
CB=CM-BM vì B nằm giữa C và M
thế 2 cái này vào biểu thức: (CA cộng CB)/2
ta có
(CM cộng AM cộng CM - BM)/2
mà AM=BM (Vì M là trung điểm của AB)
Nên biểu thức còn lại là
(CM cộng CM)/2
= (2CM)/2 =CM.
b, tương tự (mình sẽ nói ngắn gọn hơn)
ta có
CA=CM cộng AM
CB=BM-MC
nên (CA-CB)/2 = [CM cộng AM -(BM-CM)]/2
=2CM/2 = CM
29 tháng 1 2016
a) Nếu C thuộc tia đối tia BA thì BA và BC là 2 tia đối nhau
=> B nằm giữa A và C
=> AB + BC = AC
Vì M là trung điểm của AB
=> M nằm giữa A và B ; MA=MB
Vì M nằm giữa A và B
=> MA+MB = AB
Vì B nằm giữa A và C
=> BA và BC là 2 tia đối nhau
Mà M thuộc tia BA
=> BM và BC là 2 tia đối nhau
=> B nằm giữa M và C
=> MB + BC = MC
Hay AB + BC + BC = MC
AB + 2 . BC = MC
\(\frac{2\left(AB+2BC\right)}{2}=MC\)
\(\frac{\left(CA+CB\right)}{2}=MC\)
Vậy.....
vay hoi gi
ban tik minh roi lam cho