giúp mình câu này nha rất gâ rồi
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


àm ơn làm ơn hãy giúp mình câu này nha mình rất gấp rồi, mình thề sẽ quỳ gối trước bạn nào giúp mình


a: Xét ΔABM và ΔCDM có
MA=MC
\(\widehat{AMB}=\widehat{DMC}\)
MB=MC
Do đó: ΔABM=ΔCDM
a) Xét tam giác ABM và tam giác CDM có:
+ AM = CM (cho M là trung điểm của AC).
+ BM = DM (gt).
+ \(\widehat{AMB}=\widehat{CMD}\) (2 góc đối đỉnh).
\(\Rightarrow\) Tam giác ABM = Tam giác CDM (c - g - c).
b) Ta có: \(\widehat{BAM}=\widehat{DCM}\) (Tam giác ABM = Tam giác CDM).
Mà 2 góc này ở vị trí so le trong.
\(\Rightarrow\) AB // CD (dhnb).
c) Xét tam giác ABN và tam giác ECN có:
+ BN = CN (N là trung điểm của BC).
+ \(\widehat{ANN}=\widehat{ENC}\) 2 góc đối đỉnh).
+ \(\widehat{ABN}=\widehat{ECN}\) (do AB // CD).
\(\Rightarrow\) Tam giác ABN = Tam giác ECN (g - c - g).
\(\Rightarrow\) CE = AB (2 cạnh tương ứng).
Mà AB = CD (Tam giác ABM = Tam giác CDM).
\(\Rightarrow\) CE = CD (cùng = AB).
\(\Rightarrow\) C là trung điểm của DE (đpcm).
d) Xét tam giác BDE có:
+ M là trung điểm của BD (do MD = MB).
+ C là trung điểm của DE (cmt).
\(\Rightarrow\) MC là đường trung bình.
\(\Rightarrow\) MC // BE và MC = \(\dfrac{1}{2}\) BE (Tính chất đường trung bình trong tam giác).
Lại có: MC = \(\dfrac{1}{2}\) MF (do MC = MF).
\(\Rightarrow\) BE = MF.
Xét tứ giác BMEF có:
+ BE = MF (cmt).
+ BE // MF (MC // BE; C thuộc MF).
\(\Rightarrow\) Tứ giác BMEF là hình bình hành (dhnb).
\(\Rightarrow\) ME cắt BF tại trung điểm của mỗi đường (Tính chất hình bình hành).
Mà O là trung điểm của ME (gt).
\(\Rightarrow\) O là trung điểm của BF.
\(\Rightarrow\) 3 điểm B; O; F thẳng hàng (đpcm).

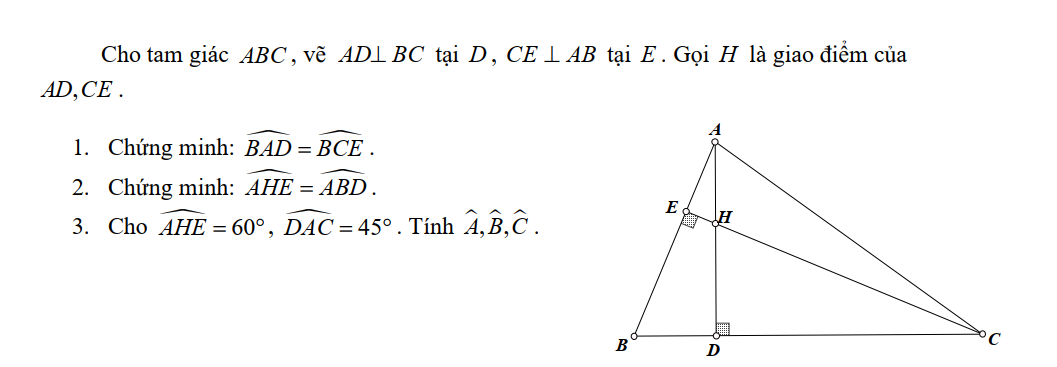
1: Ta có: \(\widehat{BAD}+\widehat{B}=90^0\)
\(\widehat{BCE}+\widehat{B}=90^0\)
Do đó: \(\widehat{BAD}=\widehat{BCE}\)
2: Ta có: \(\widehat{AHE}+\widehat{BAD}=90^0\)
\(\widehat{ABD}+\widehat{BAD}=90^0\)
Do đó: \(\widehat{AHE}=\widehat{ABD}\)

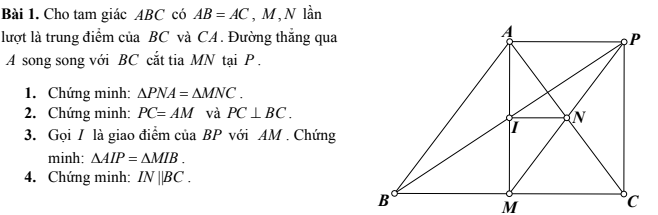
4: Xét ΔAMC có
I là trung điểm của AM
N là trung điểm của AC
Do đó: IN là đường trung bình của ΔAMC
Suy ra: IN//MC
hay IN//BC

1: Xét ΔABC có AB=AC
nên ΔABC cân tại A
Suy ra: \(\widehat{B}=\widehat{C}\)
Ta có: ΔBAC cân tại A
mà AH là đường trung tuyến ứng với cạnh đáy BC
nên AH là đường cao ứng với cạnh BC

1. Tam giác AOC và tam giác BOD có: AO = BO; CO = DO: góc AOC = góc BOD (đối đỉnh)
--> tam giác AOC = tam giác BOD (c.g.c)
--> góc ACO = góc ODB
Mà 2 góc này ở vị trí so le trong
--> AC // BD

Áp dụng t/c dtsbn:
\(a+b+c=\dfrac{c}{a+b+1}=\dfrac{a}{b+c+2}=\dfrac{b}{a+c-3}=\dfrac{a+b+c}{2a+2b+2c}=\dfrac{1}{2}\\ \Rightarrow\left\{{}\begin{matrix}a+b+c=\dfrac{1}{2}\\2c=a+b+1\\2a=b+c+2\\2b=a+c-3\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}a+b+c+1=3c\\a+b+c+2=3a\\a+b+c-3=3b\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}3c=\dfrac{3}{2}\\3a=\dfrac{5}{2}\\3b=-\dfrac{5}{2}\end{matrix}\right.\\ \Rightarrow\left\{{}\begin{matrix}c=\dfrac{1}{2}\\a=\dfrac{5}{6}\\b=-\dfrac{5}{6}\end{matrix}\right.\)


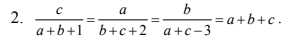 tìm a, b, c
tìm a, b, c
24 giờ
B