Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Vật chuyển động tròn đều trên một đường tròn có \(R\) không đổi.
Nếu vật chuyển động tròn đều với tốc độ góc là \(2\omega\) trên cùng đường tròn đó (cùng \(R\)) thì gia tốc hướng tâm là:
\(a'_{ht}=R\cdot\omega'^2=R\cdot\left(2\omega\right)^2=R\cdot4\omega^2\)
Mà \(a_{ht}=R\cdot\omega^2\)
\(\Rightarrow a'_{ht}=4a_{ht}\)
Chọn đáp án B
+ Áp dụng công thức
+ Vận tốc dài: 
+ Gia tốc hướng tâm:
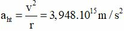
sau 20 s vật quay được 10 vòng
⇒ 1s vật quay được 0,5 vòng
⇒ f = 0,5 vòng/s
ta có \(T=\dfrac{1}{f}=\dfrac{1}{0,5}=2s\)
b, đổi 20cm = 0,2 m
\(T=\dfrac{2\text{π}}{\text{ω}}\)⇒ω\(=\dfrac{2\text{π}}{T}\)\(=\dfrac{2\text{π}}{2}\)\(=\text{π}\) rad/s
\(v=r\text{ω}\)\(=0,2\text{π}\)
c, \(a_{ht}=\dfrac{v^2}{r}=\dfrac{0,4\text{π}^2}{0,2}=0,2\text{π}^2\)
Đổi 30 cm =0,3 m; 1 phút =60s
a,\(T=\dfrac{1}{f}=\dfrac{1}{\dfrac{N}{t}}=\dfrac{1}{\dfrac{60}{60}}=1\left(s\right)\)
\(\omega=\dfrac{2\pi}{T}=2\pi\left(\dfrac{rad}{s}\right)\)
b,\(v=\dfrac{2\pi}{T}\cdot r=0,6\pi\left(\dfrac{m}{s}\right)\)
\(a_{ht}=\dfrac{v^2}{r}=\dfrac{\left(0,6\pi\right)^2}{0,3}=1,2\pi^2\left(\dfrac{m}{s^2}\right)\)
c, Đổi 10 cm =0,1m
Khoảng cách từ tâm đến điểm được xét =0,3-0,1=0,2(m)
<Rùi tính tiếp>
\(v'=\dfrac{2\pi}{T}r'=0,4\pi\left(\dfrac{m}{s}\right)\)
\(a_{ht}'=\dfrac{v'^2}{r'}=\dfrac{\left(0,4\pi\right)^2}{0,3}=\dfrac{8}{15}\pi^2\left(\dfrac{m}{s^2}\right)\)
Đáp án A
Trong chuyển động quay của vật rắn quanh một trục cố định thì các điểm trên vật luôn chuyển động cùng tốc độ góc