Cho hình hộp ABCD.A'B'C'D'. Gọi I và I' lần lượt là tâm của ABB'A' và DCC'D'. Mệnh đề nào sau đây là sai?
A. I I ' → = A D →
B. I I ' / / ( A D D ' A ' )
C. II' và BB' cùng nằm trong một mặt phẳng
D. II' và DC không có điểm chung
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
20 tháng 8 2019
Đáp án C.
+ ADC'B' là hình bình hành.
+ II'//AD => II'//(ADD'A') và I I ' ⇀ = A D ⇀ nên đáp án A, B là đúng.
+ II'//(ABCD) nên II' và DC không có điểm chung nên đáp án D đúng.
+ (ABB'A') // (BCC'B') = BB' và 
tức là II' và BB' không cùng thuộc một mặt phẳng nên đáp án C sai.
CM
6 tháng 3 2018
Đáp án D
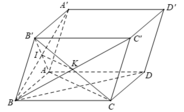
+) A đúng do tính chất đường trung bình trong ΔB'AC và tính chất của hình bình hành ACC'A'.
+) B đúng do IK // AC nên bốn điểm I, K, C, A đồng phẳng.
+) C đúng do việc ta phân tích:
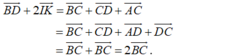
+) D sai do giá của ba vectơ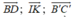 
đều song song hoặc trùng với mặt phẳng (ABCD). Do đó, theo định nghĩa sự đồng phẳng của các vectơ, ba vectơ trên đồng phẳng.
CM
27 tháng 12 2019
Chọn D.
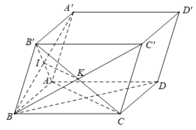
+) A đúng, vì:
- Tam giác B’AC có IK là đường trung bình của tam giác nên
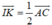
- Tứ giác ACC’A’ là hình bình hành nên
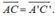
+) B đúng, vì 4 điểm I, K, C, A cùng thuộc mp(B’AC).
+) C đúng, vì:
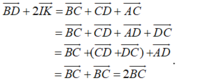
+) D sai do giá của ba vectơ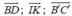 
đều song song hoặc trùng với mặt phẳng (ABCD). Do đó, theo định nghĩa sự đồng phẳng của các vectơ, ba vectơ trên đồng phẳng.
CM
22 tháng 4 2018
Đáp án A
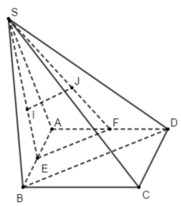
Tam giác SAB có I là trọng tâm và E là trung điểm của AB
Nên ta có S I S E = 2 3 (1)
Tam giác SAD có J là trọng tâm và F là trung điểm của AD
Nên ta có S J S F = 2 3 (2)
Từ (1) và (2) ta có: IJ // EF (3) (định lý Ta-lét trong tam giác SEF)
Tam giác ABD có EF là đường trung bình nên EF // BD (4)
Từ (3) và (4) suy ra IJ // BD
Mà BD (SBD)
Do đó IJ // (SBD).
CM
15 tháng 8 2017
Đáp án A
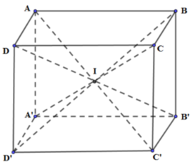
Phương pháp:
Xác định tỉ số chiều cao và tỉ số diện tích đáy của chóp I.ABCD và khối hộp ABCD.A’B’C’D’.
Cách giải:
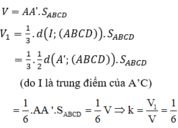
Đáp án C.
Ta có MN//AC và NP//SC ⇒ (MNP)//(SAC) nên đáp án A đúng.
Do B D ⊥ S A và B D ⊥ A C ⇒ B D ⊥ ( S A C ) nên đáp án B đúng.
Do B C ⊥ A B và B C ⊥ S A ⇒ B C ⊥ ( S A B ) ⇒ B C ⊥ M P nên đáp án D đúng.
Vậy đáp án C sai.