Cho hàm số y = a x + b c x + d có đồ thị như hình vẽ bên, trong đó d < 0 . Mệnh đề nào dưới đây là mệnh đề đúng?
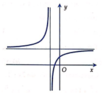
A. a < 0, b < 0, c < 0
B. a > 0, b < 0, c > 0
C. a<0, b>0,c<0
D. a > 0, b > 0, c > 0
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn đáp án B.
Từ đồ thị hàm số, ta có: giao điểm của đồ thị hàm số với trục tung nằm phía trên trục hoành nên b d > 0
Tiệm cận đứng của đồ thị nằm bên phải trục tung nên - d c < 0
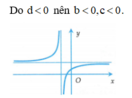

Đáp án B.
Từ đồ thị ta có:
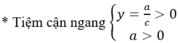
Loại b > 0, c < 0, d < 0 và b < 0, c < 0, d < 0. Còn lại b > 0, c > 0, d < 0; b <0, c > 0, d < 0.
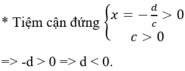
* Cho x = 0 => y = b/d < 0 => b > 0. Đáp án B > 0, c > 0, d < 0.

Đáp án C.
Đồ thị hàm bậc bốn trùng phương có dạng chữ M nên suy ra a <0 .
Đồ thị hàm số cắt trục Oy tại điểm (0;c) nên suy ra c < 0.
Hàm số có ba cực trị nên suy ra ab < 0 , (a, b trái dấu). Mà a < 0 nên suy ra b > 0.
Vậy C là đáp án đúng.
Đáp án A.
Cách 1: Từ đồ thị, ta có b d = y 0 > 0 . Suy ra b < 0 .
Lại có y = 0 ⇔ x = − b a < 0 . Suy ra a < 0 . Do đó đáp án đúng là A.
Cách 2: Từ đồ thị, ta có đường tiệm cận đứng x = − d c < 0 và tiệm cận ngang y = a c > 0 . Do d < 0 nên c < 0 . Suy ra a < 0 .
Lại do b d = y 0 > 0 nên suy ra b < 0 . Do đó đáp án đúng là A.