 ai giải giúp em mấy bài toán này vs ạ giải chi tiết giúp em ạ
ai giải giúp em mấy bài toán này vs ạ giải chi tiết giúp em ạ
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(M=\dfrac{\sqrt{x}+3}{\sqrt{x}-3}\left(đk:x\ge0,x\ne9\right)\)
Để \(M=\dfrac{\sqrt{x}+3}{\sqrt{x}-3}< 0\) thì
\(\sqrt{x}-3< 0\) ( do \(\sqrt{x}+3\ge3>0\))
\(\Leftrightarrow\sqrt{x}< 3\Leftrightarrow0\le x< 9\)
Mà \(x\in Z\)
\(\Rightarrow x\in\left\{0;1;2;3;4;5;6;7;8\right\}\)


Câu 40. \(n_{NaOH}=\dfrac{20}{40}=0,5\left(mol\right);n_{HCl}=\dfrac{36,5}{36,5}=1\left(mol\right)\)
PTHH: \(NaOH+HCl\rightarrow NaCl+H_2O\)
Theo đề: 0,5mol .....1mol
Lập tỉ lệ : \(\dfrac{0,5}{1}< \dfrac{1}{1}\)=> Sau phản ứng NaOH hết, HCl dư
=> Thử môi trường sau phản ứng bằng quỳ sẽ có màu đỏ
Câu 41.
nNaOH=0,3.0,5=0,15(mol);nHCl=0,3.1=0,3(mol)
PTHH: NaOH + HCl → NaCl + H2O
Theo đề:0,15mol ....0,3mol
Lập tỉ lệ :\(\dfrac{0,15}{1}< \dfrac{0,3}{1}\)=> Sau phản ứng NaOH hết, HCl dư
=> Dung dịch sau phản ứng làm quỳ tím hóa màu đỏ

24.
Đường thẳng có 1 vtcp là \(\overrightarrow{u}=\left(2;-5\right)\)
25.
\(a^2=b^2+c^2-2bc.cosA\)
26.
A là mệnh đề sai, công thức đúng: \(S=\dfrac{1}{2}ab.sinC\)
27.
\(BC=\sqrt{AB^2+AC^2-2AB.AC.cosA}=\sqrt{3^2+4^2-2.3.4.cos60^0}=\sqrt{13}\)
28.
\(\widehat{A}=180^0-\left(35^030'+45^0\right)=99^030'\)
Áp dụng định lý hàm sin:
\(\dfrac{a}{sinA}=\dfrac{b}{sinB}\Rightarrow b=\dfrac{a.sinB}{sinA}=\dfrac{12,5.sin\left(35^030'\right)}{sin\left(99^030'\right)}=7,36\left(m\right)\)

Câu 3:
a) Lưu huỳnh (S) có hóa trị II. Hidro (H) có hóa trị I.
-> Ta sẽ có hợp chất: \(H^I_aS^{II}_b\) (a,b: nguyên, dương)
Theo quy tắc hóa trị ta có:
I.a=II.b
=>a/b=II/I=2/1
=>a=2; b=1
=> CTHH là H2S
Câu 3b)
- Na có hóa trị (I) và CO3 có hóa trị (II).
- Ta đặt: \(Na^I_x\left(CO_3\right)^{II}_y\) (x,y: nguyên, dương)
Theo QT hóa trị ta sẽ có được:
x.I=II.y
<=>x/y=II/I=2/1
=>x=2; y=1
=> CTHH sẽ là Na2CO3

\(\left\{{}\begin{matrix}6u_2+u_5=1\\3u_3+2u_4=-1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}6u_1.q+u_1.q^4=1\\3u_1.q^2+2u_1.q^3=-1\end{matrix}\right.\)
\(\Rightarrow u_1\left(6q+q^4+3q^2+2q^3\right)=0\)
\(\Leftrightarrow q^3+2q^2+3q+6=0\)
\(\Leftrightarrow\left(q+2\right)\left(q^2+3\right)=0\)
\(\Leftrightarrow q=-\text{}2\)
\(\Rightarrow u_1=\dfrac{1}{4}\)
\(\Rightarrow u_n=u_1.q^{n-1}=\dfrac{1}{4}.\left(-2\right)^{n-1}=\left(-2\right)^{n-3}\)

\(x=\left(\dfrac{1}{2}\right)^3:\left(\dfrac{1}{2}\right)=\left(\dfrac{1}{2}\right)^{3-1}=\left(\dfrac{1}{2}\right)^2=\dfrac{1}{4}\)


 ai giải giùm em câu 6 vs ạ cho em lời giải chi tiết và vẽ hình giúp em vs ạ cảm ơn mn
ai giải giùm em câu 6 vs ạ cho em lời giải chi tiết và vẽ hình giúp em vs ạ cảm ơn mn



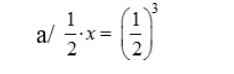 giúp em bài này với ạ,giải chi tiết luôn nha,em cảm ơn
giúp em bài này với ạ,giải chi tiết luôn nha,em cảm ơn
\(1,\\ a,=6x^4y^4-x^3y^3+\dfrac{1}{2}x^4y^2\\ b,=4x^3+5x^2-8x^2-10x+12x+15\\ =4x^3-3x^2+2x+15\\ 2,\\ a,=7\left(x^2-6x+9\right)=7\left(x-3\right)^2\\ b,=\left(x-y\right)^2-36=\left(x-y-6\right)\left(x-y+6\right)\\ 3,\\ \Leftrightarrow x\left(x^2-0,36\right)=0\\ \Leftrightarrow x\left(x-0,6\right)\left(x+0,6\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=0\\x=0,6\\x=-0,6\end{matrix}\right.\)
cảm ơn bạn minh nhiều nha