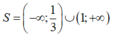Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
hoc gioi the hihiihihihhhihihihihiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiii
,mnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnn
Đáp án C.
- Phương pháp:
+) Tính f'(x).
+) Sử dụng quy tắc trong trái ngoài cùng giải bất phương trình bậc hai.
- Cách giải:
+ Ta có:
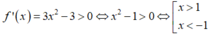
→ Vậy tập nghiệm của bất phương trình là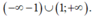 
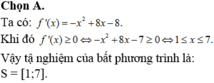
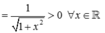
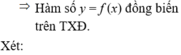
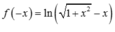
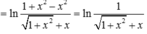
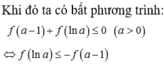
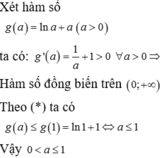
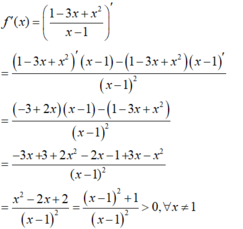
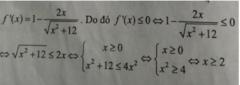
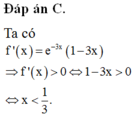
Chọn A
+ Xét x ≥ 1/2 thì ta có nhị thức f(x) = x-1 để f(x) > 0 thì x> 1
Vậy với x > 1 thỏa mãn bpt đã cho.
+ Xét x < 1/2 thì ta có nhị thức f(x)= –3x+ 1 để f(x) > 0 thi x< 1/3
Vậy x < 1/3 thỏa mãn bpt đã cho.
Vậy tập nghiệm của bất phương trình đã cho là