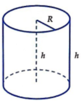
Trong các khối trụ có thể tích V không đổi thì hình trụ có diện tích toàn phần lớn nhất khi tỉ lệ giữa chiều cac h và bán kính đáy R là:
A . h R = 1
B . h R = 2
C . h R = 2
C . h R = 1 2
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B.
Ta có: V = π R 2 h ⇒ h = V π R 2 (1)
S x q = 2 π R h = 2 π . R . V π R 2 = 2 V R ; S t p = S x q + 2 S đ = 2 V R + 2 π R 2
Xét hàm số f R = 2 V R + 2 π R 2 (V là hằng số)
f ' R = − 2 V R 2 + 4 π R = 0 ⇔ R = V 2 π 3
Bảng biến thiên:
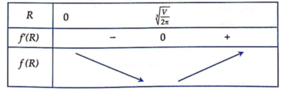
⇒ S t p min = f R min ⇔ R = V 2 π 3 ⇒ v = 2 π R 3
Từ (1)
⇒ h = V π R 2 = 2 π R 3 π R 2 = 2 R ⇒ h R = 2

Đáp án B
Phương pháp giải: Chuẩn hóa thể tích, đưa diện tích toàn phần về hàm số, khảo sát hàm (hoặc bất đẳng thức) tìm min
Lời giải:
Thể tích của khối trụ là 
Chuẩn hóa 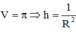
Diện tích toàn phần của hình trụ là ![]()
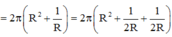
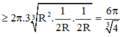
Dấu bằng xảy ra khi và chỉ khi ![]()

Đáp án D
Lời giải:

Lập bảng biến thiên ta thấy h0 là điểm cực đại của hàm số f(h) và f(h0) là GTLN của f(h) trên (0;2R)

a) Giá trị gần đúng của h là : 10,5 cm
b) Giá trị của r là : 24 cm
Đáp án B.
Ta có:
Xét hàm số
Bảng biến thiên: