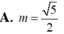
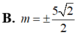
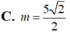
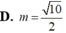
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
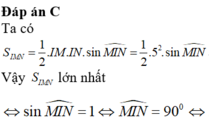
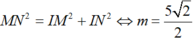
Đáp án C
Ta có:
S I M N = 1 2 . I M . I N . sin M I N ^ = 1 2 .5 2 . sin M I N ^ .
Vậy S I M N lớn nhất ⇔ sin M I N ^ = 1
⇔ M I N ^ = 90 0 ⇔ M N 2 = I M 2 + I N 2 ⇔ m = 5 2 2
Chọn C
.
Vì 
nên phương trình 
có 2 nghiệm phân biệt.
Do đó hàm số có hai điểm cực trị 
.
Giả sử hàm số có hai điểm cực trị lần lượt là 
và 
, với 
, 
là nghiệm của phương trình 
.
Thực hiện phép chia 
cho 
ta được : 
.
Khi đó ta có: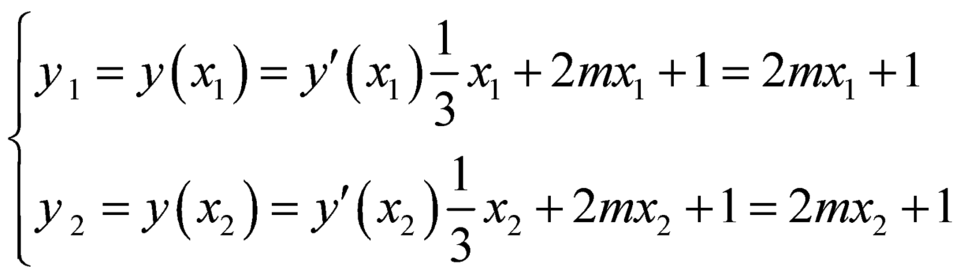 
.
Ta thấy, toạ độ hai điểm 
và 
thoả mãn phương trình 
.
Do đó, phương trình đường thẳng qua hai điểm cực trị là 
.
Ta thấy 
luôn qua 
.
Đặt 
.
.
Xét hàm số 
, 
.
, 
.
Suy ra hàm số 
liên tục và đồng biến trên 
.
Do đó 
.
Vậy 
đạt giá trị lớn nhất 
.
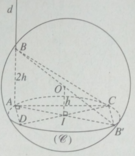
Diện tích tam giác BCD bằng:
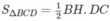
Diện tích này lớn nhất khi AI // CD.
Đáp án C
Ta có: II' = 6 = R + R'
Ta có: MN ≥ MI + II' + I'N = R + 6 + R' = 12
Dấu bằng xảy ra khi M, I, I', N theo thứ tự nằm trên một đường thẳng. Do đó M là giao điểm của tia đối của tia II' với mặt cầu (S), N là giao điểm của tia đối của tia I’I với mặt cầu (S’). Vậy đáp án đúng là C.
( hình như bài này còn cách khác nữa ...) 