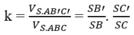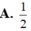
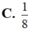
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
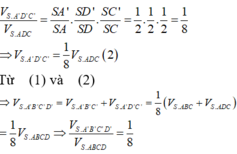
Đáp án C
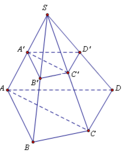
Ta có: V S . A ' B ' C ' V S . A B C = S A ' S A . S B ' S B . S C ' S C = 1 2 . 1 2 . 1 2 = 1 8
⇒ V S . A ' B ' C ' = 1 8 V S . A B C 1
V S . A ' D ' C ' V S . A D C = S A ' S A . S D ' S D . S C ' S C = 1 2 . 1 2 . 1 2 = 1 8
⇒ V S . A ' D ' C ' = 1 8 V S . A D C 2
Từ (1) và (2) ⇒ V S . A ' B ' C ' D ' = V S . A ' B ' C ' + V S . A ' D ' C ' = 1 8 V S . A B C + V S . A D C
= 1 8 V S . A B C D ⇒ V S . A ' B ' C ' D ' V S . A B C D = 1 8
Đáp án C
Ta có V S . A ' B ' C ' V S . A B C = S A ' S A . S B ' S B . S C ' S C = 1 8 và V S . A ' D ' C ' V S . A D C = S A ' S A . S D ' S D . S C ' S C = 1 8
Mà V S . A B C = V S . A D C = 1 2 V S . A B C D ⇒ V S . A ' B ' C ' + V S . A ' D ' C ' = V S . A B C D 8 ⇔ V S . A ' B ' C ' D ' V S . A B C D = 1 8 .
Đáp án C
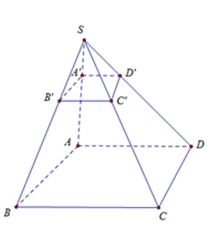
Dễ thấy hình chóp S.A'B'C'D' đồng dạng với hình chópS.ABCD theo tỷ số k = 1 3
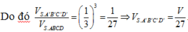
Chọn C.
Dễ thấy BD ⊥ SC, nên BD // (AB'C'D'), suy ra BD // B'D'.
Gọi I = AC ∩ BD, J = AC' ∩ SI, khi đó J là trọng tâm của tam giác SAC và J ∈ B'D'.
Suy ra
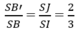
Do đó dễ thấy
