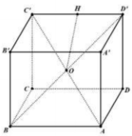
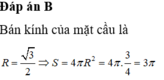Mặt cầu đi qua tất cả các đỉnh của hình lập phương cạnh a có bán kính bằng
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Tâm là giao điểm các đường chéo (O)
Bán kính mặt cầu là OA = 1/2 AC’
Đường chéo hình vuông cạnh a là a√2 (AC = a√2)
Xét tam giác vuông ACC’ tại C:
⇒ bán kính mặt cầu đi qua 8 đỉnh hình lập phương là (a√3)/2

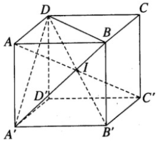
Gọi I là tâm của hình lập phương. Tất cả các đỉnh của hình lập phương đều có khoảng cách đến I bằng 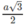 nên chúng nằm trên mặt cầu tâm I bán kính
nên chúng nằm trên mặt cầu tâm I bán kính 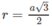
Ta có diện tích mặt cầu đó là S = 4 πr 2 = 3 πa 2

Đáp án B
Bán kính của mặt cầu là
R = 3 2 ⇒ S = 4 π R 2 = 4 π . 3 4 = 3 π

Đáp án A
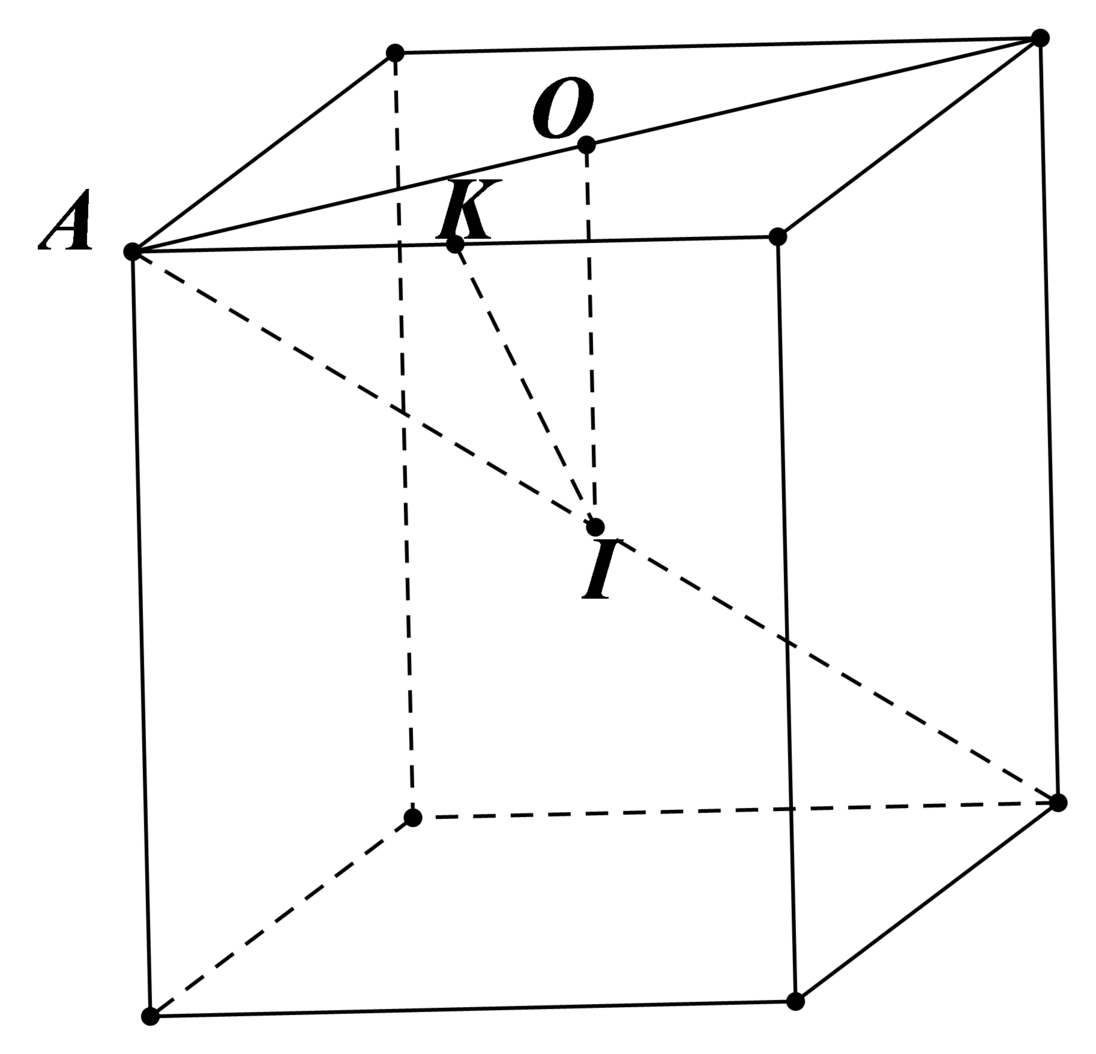
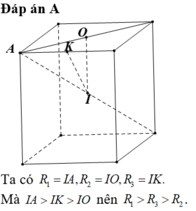
Ta có: R 1 = I A , R 2 = I O , R 3 = I K . Mà I A > I K > I O nên R 1 > R 3 > R 2 .