Cho I = ∫ 1 2 2 x x 2 - 1 d x và u = x2 – 1. Chọn khẳng định sai trong các khẳng định sau:
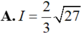
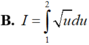
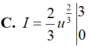
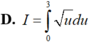
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B
Ta có lim x → - 1 x 2 - 1 x + 1 = lim x → - 1 x - 1 x + 1 x + 1 = lim x → - 1 x - 1 = - 2 = f - 1 ⇒ Hàm số f(x) liên tục trên ℝ

Ta có: y(0) = 0-1= - 1
Và y(-2) = -2 – 1 = - 3
*Xét tính liên tục của hàm số tại x=1
lim x → 1 + y = lim x → 1 + x 2 + 3 x + 1 x − 1 = + ∞ x → 1 + : x − 1 > 0 ; lim x → 1 + ( x − 1 ) = 0 lim x → 1 + ( x 2 + 3 x + 1 ) = 5 > 0
Và lim x → 1 − y = lim x → 1 − ( x − 1 ) = 0
⇒ lim x → 1 + y ≠ lim x → 1 − y
Do đó, hàm số đã cho không liên tục tại x =1
Suy ra, hàm số cũng không có đạo hàm tại x = 1
Chọn D.

Chọn B.
D = [-2; 2]
F(x) không xác định tại x = 3
![]() ; f(-2) = 0. Vậy hàm số liên tục tại x = -2
; f(-2) = 0. Vậy hàm số liên tục tại x = -2
![]()
Vậy không tồn tại giới hạn của hàm số khi x → 2.

+ Trên (-1; +∞), f ( x ) = x 2 - 1 là hàm đa thức nên hàm số liên tục trên khoảng đó.
+ Trên (-∞; -1), f(x) = 3x + 2 là hàm đa thức nên hàm số liên tục trên (-∞; -1).
- Ta xét tính liên tục của hàm số tại điểm x = -1:
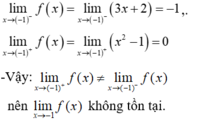
- Do đó f(x) không liên tục tại x= -1 nên A, B, D sai.
Chọn C.
Chọn B