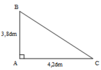
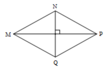
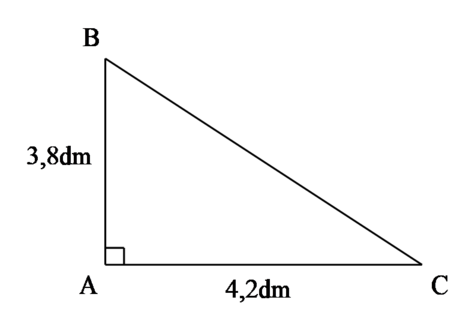Cho MP = 6cm và NQ = 3cm.Diện tích của hình ABCD là :…………Diện tích của hình MNPQ là
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
CM
Cao Minh Tâm
9 tháng 3 2018
Đúng(0)
Những câu hỏi liên quan
PT
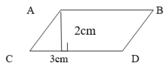
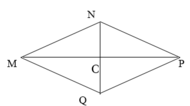
Cho MP = 6cm và NQ = 3cm.
Diện tích của hình ABCD là ……………….
Diện tích của hình MNPQ là ……………………………..
1
CM
11 tháng 10 2017
Diện tích của hình ABCD là 6cm2
Diện tích của hình MNPQ là 9cm2
NQ
1
CM
24 tháng 3 2019
a, Diện tích hình tam giác ABC là:
3,8 × 4,2 2 = 7,98 dm 2
b, MP = 5,8dm = 58cm
NQ = 56cm
Diện tích hình thoi MNPQ là:
58 × 56 2 = 1624 cm 2
Đáp số:
a) 7,98 d m 2
b) 1624 c m 2
PT
1
CM
4 tháng 1 2020
a) Diện tích hình tam giác ABC là:
3,8 × 4,2 2 = 7,98 dm 2
b) MP = 5,8dm = 58cm ; NQ = 56cm
Diện tích hình thoi MNPQ là:
58 × 56 2 = 1624 cm 2
Đáp số: a) 7,98 d m 2 ; b) 1624 c m 2
AH
Akai Haruma
Giáo viên
10 tháng 5 2021
Lời giải:
$S_{MNQ}=S_{MNP}$ (do chiều cao bằng nhau và chung đáy)
$\Rightarrow S_{MQK}=S_{NKP}=15$ (cm2)
Kẻ đường cao $NH$ xuống $MP$, đường cao $QT$ xuông $MH$
\(\frac{S_{MNP}}{S_{MQP}}=\frac{MN}{PQ}=\frac{3}{5}\)
\(\frac{S_{MNP}}{S_{MQP}}=\frac{NH}{QT}\)
\(1=\frac{S_{NPK}}{S_{MQK}}=\frac{NH\times PK}{QT\times MK}\Rightarrow \frac{NH}{QT}=\frac{MK}{PK}\)
Từ 3 điều trên suy ra $\frac{MK}{PK}=\frac{3}{5}$
$\frac{S_{MNK}}{S_{NPK}}=\frac{MK}{PK}=\frac{3}{5}$
$S_{MNK}=\frac{3}{5}\times S_{NPK}=\frac{3}{5}\times 15=9$ (cm2)
$\frac{S_{MQK}}{S_{PQK}}=\frac{MK}{PK}=\frac{3}{5}$
$\Rightarrow S_{PQK}=\frac{5}{3}\times S_{MQK}=\frac{5}{3}\times 15=25$ (cm2)
Diện tích hình thang:
$15+15+9+25=64$ (cm2)
5 tháng 5 2018
giải
độ dài đường chéo MP là:
72 : 4 = 18 (cm)
độ dài đường chéo NQ là:
18 x 2/3 = 12 (cm)
Diện tích hình thoi MNPQ là:
1/2 x ( 18 x 12) = 108 ( cm2)
5 tháng 5 2018
bằng 108 nhé
vì một cạnh hinh vuông là 18 còn đường chéo thứ2 bằng 18 X 2/3 bằng 12 diện tích là (12 X18) :2 = 108 cm