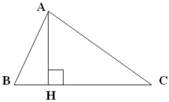
Cho tam giác ABC (như hình vẽ)
Điền vào chỗ trống
a) Đoạn thẳng vuông góc với BC là:
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
9 tháng 3 2019
a. Đường thẳng vuông góc với BC là .......AH
b. Vẽ thêm một cạnh song song với cạnh BC.
CM
4 tháng 1 2017
a) Xét tứ giác ADME có:
∠(DAE) = ∠(ADM) = ∠(AEM) = 90o
⇒ Tứ giác ADME là hình chữ nhật (có ba góc vuông).
b) Ta có ME // AB ( cùng vuông góc AC)
M là trung điểm của BC (gt)
⇒ E là trung điểm của AC.
Ta có E là trung điểm của AC (cmt)
Chứng minh tương tự ta có D là trung điểm của AB
Do đó DE là đường trung bình của ΔABC
⇒ DE // BC và DE = BC/2 hay DE // MC và DE = MC
⇒ Tứ giác CMDE là hình bình hành.
c) Ta có DE // HM (cmt) ⇒ MHDE là hình thang (1)
Lại có HE = AC/2 (tính chất đường trung tuyến của tam giác vuông AHC)
DM = AC/2 (DM là đường trung bình của ΔABC) ⇒ HE = DM (2)
Từ (1) và (2) ⇒ MHDE là hình thang cân.
d) Gọi I là giao điểm của AH và DE. Xét ΔAHB có D là trung điểm của AB, DI // BH (cmt) ⇒ I là trung điểm của AH
Xét ΔDIH và ΔKIA có
IH = IA
∠DIH = ∠AIK (đối đỉnh),
∠H1 = ∠A1(so le trong)
ΔDIH = ΔKIA (g.c.g)
⇒ ID = IK
Tứ giác ADHK có ID = IK, IA = IH (cmt) ⇒ DHK là hình bình hành
⇒ HK // DA mà DA ⊥ AC ⇒ HK ⊥ AC
CM
15 tháng 4 2017
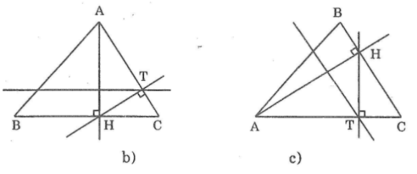
Hình a sai ; Hình b đúng ; Hình c đúng ; Hình d sai
Tên các điểm được thể hiện trong hình dưới:
4 tháng 1 2023
a: Xét tứ giác ADME có
góc ADM=góc AEM=góc DAE=90 độ
nên ADME là hình chữ nhật
b: Xét ΔABC có ME//AB
nên CE/CA=CM/CB=1/2
=>E là trung điểm của AC
Xét ΔCAB có MD//AC
nên MD/AC=BD/BA=BM/BC=1/2
=>D là trung điểm của BA
=>MD//CE và MD=CE
=>MCED là hình bình hành
c: Xét ΔABC có AD/AB=AE/AC
nên DE//BC
=>DE//HM
ΔHAC vuông tại H
mà HE là đường trung tuyến
nên HE=AC/2=MD
Xét tứ giác MHDE có
MH//DE
MD=HE
Do đó;MHDE là hình thang cân
22 tháng 5 2022
a) Xét tứ giác ADME có:
∠(DAE) = ∠(ADM) = ∠(AEM) = 90o
⇒ Tứ giác ADME là hình chữ nhật.
b) Ta có ME // AB ( cùng vuông góc AC)
M là trung điểm của BC (gt)
⇒ E là trung điểm của AC.
Ta có E là trung điểm của AC (cmt)
Chứng minh tương tự ta có D là trung điểm của AB
Do đó DE là đường trung bình của ΔABC
⇒ DE // BC và DE = BC/2 hay DE // MC và DE = MC
⇒ Tứ giác CMDE là hình bình hành.
22 tháng 5 2022
a: Xét tứ giác ADME có \(\widehat{ADM}=\widehat{AEM}=\widehat{DAE}=90^0\)
nên ADME là hình chữ nhật
b: Xét ΔCAB có
M là trung điểm của BC
ME//AB
Do đó: E là trung điểm của AC
Xét tứ giác CEDM có
DM//CE
DM=CE
Do đó: CEDM là hình bình hành
c: Ta có: ΔAHC vuông tại H
mà HE là đường trung tuyến
nên HE=AC/2=MD
Xét ΔABC có
M là trung điểm của BC
MD//AC
Do đó: D là trung điểm của AB
Xét ΔBAC có
E la trung điểm của AC
D là trung điểm của AB
Do đó: ED là đường trung bình
=>ED//BC
hay ED//MH
=>EMHD là hình thang
mà EH=MD
nên EMHD là hình thang cân
18 tháng 7 2018
a)ta có: góc EAC = góc DAB ( = 90 độ)
=> góc EAC + góc BAC = góc DAB + góc BAC
=> góc EAB = góc DAC
Xét tam giác EAB và tam giác CAD
có: EA = CA ( gt)
góc EAB = góc CAD ( cmt)
AB = AD ( gt)
\(\Rightarrow\Delta EAB=\Delta CAD\left(c-g-c\right)\)
=> EB = CD ( 2 cạnh tương ứng)
( Gọi giao điểm của EB và CD là O; giao điểm của CD và AB là H)
ta có: \(\Delta EAB=\Delta CAD\left(cmt\right)\)
=> góc EBA = góc CDA ( 2 góc tương ứng)
Xét tam giác ADH vuông tại A
có: góc CDA + góc AHD = 90 độ ( 2 góc phụ nhau)
mà góc EBA = góc CDA ( cmt)
góc AHD = góc OHB ( đối đỉnh)
=> góc CDA + góc AHD = góc EBA + góc OHB = 90 độ
=> góc EBA + góc OHB = 90 độ
mà góc EBA, góc OHB là 2 góc phụ nhau
\(\Rightarrow DC\perp BE⋮O\) ( định lí)
b) Xét tam giác EMN và tam giác DAN
có: MN = AN ( gt)
góc ENM = góc DNA ( đối đỉnh)
EN = DN (gt)
\(\Rightarrow\Delta EMN=\Delta DAN\left(c-g-c\right)\)
=> EM = DA ( 2 cạnh tương ứng)
mà DA = AB
=> EM = AB ( = DA)
...
xl bn nha, nhưng mk chỉ bk chứng minh đến đây thoy!
NT
18 tháng 7 2018
a) Ta có: góc DAC= góc DAB + góc BAC
góc BAE= góc EAC+ góc CAB
Mà góc DAB= góc EAC=90 độ
=> góc DAC= góc BAE
Xét tam giác DAC và tam giác BAE có:
AD=AB
góc DAC= góc BAE
AC=AE
=> tam giác DAC= tam giác BAE ( c.g.c)
=> DC=BE
Gọi I và H lần lượt là giao điểm của DC với AB và BE
Ta có: góc D+ góc DAH+ góc DHA= góc B+ góc BHI+ góc BIH= 180 độ
Mà góc D= góc B ( tam giác DAC= tam giác BAE) va góc DHA = góc BHI ( hai góc đôi đỉnh)
=> góc DAH= góc BIH
Mà góc DAH=90 độ=> góc BIH=90 độ=> DC vuông góc vs BE
b,
Xét tam giác ADN và tam giác MEN có:
DN=NE (gt)
góc N1= góc N2 ( đ đ )
AN=MN ( gt)
Suy ra tam giác ADN = tam giác MEN (c.g.c)
Suy ra DA=ME Mà DA = AB ( gt) suy ra ME=AB
Ta có;góc DAB + góc EAC = 180 độ
Suy ra Góc A1 + góc A2 =180 độ ( 1 )
Mặt khác tam giác ADN = tam giác MEN suy ra góc E1 = góc D1
Suy ra ME song song vs AD ( 2 góc SLT)
Suy ra góc MEA + góc A2 =180 độ ( TCP ) ( 2 )
Từ 1 và 2 suy ra góc MEA = góc A1
và ME = AB (gt) ; AE = AC (cmt)
Suy ra Tam giác AME = Tam giác CBA ( c.g.c)
AH