Cho khối tứ diện ABCD. M, N lần lượt là trung điểm của BC và BD. Mặt phẳng (AMN). chia khối tứ diện ABCD thành
A. Một khối tứ diện và một khối chóp tứ giác
B. Hai khối tứ diện
C. Hai khối tứ diện và một khối chóp tứ giác
D. Hai khối chóp tứ giác
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn A.
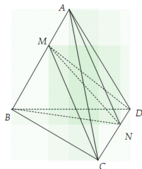
Nhìn vào hình vẽ ta thấy MN là giao tuyến của hai mặt phẳng (MCD) và (NAB), khi đó ta thấy tứ diện đã cho được chia thành bốn tứ diện ACMN, AMND, BMNC, BMND.

Chọn A.
Nhìn vào hình vẽ ta thấy MN là giao tuyến của hai mặt phẳng (MCD) và (NAB), khi đó ta thấy tứ diện đã cho được chia thành bốn tứ diện ACMN,AMND,BMNC,BMND.
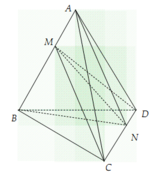

Đáp án A
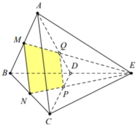
Nối ![]() chia khối tứ diện ABCD thành hai khối đa diện gồm PQD.NMB và khối đa diện chứa đỉnh A có thể tích A.
chia khối tứ diện ABCD thành hai khối đa diện gồm PQD.NMB và khối đa diện chứa đỉnh A có thể tích A.
Dễ thấy P,Q lần lượt là trọng tâm của ∆BCE, ∆ABE
Gọi S là diện tích 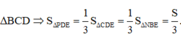
Họi h là chiều cao của tứ diện ABCD 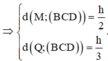
Khi đó 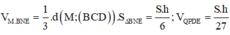
Suy ra
![]()
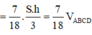


Đáp án D
Áp dụng công thức tính tỉ số thể tích, ta có
V A . B ' C D ' V A . B C D = A B ' A B . A C A C . A D ' A D = 1 4
⇔ V A . B ' C D ' = V 4
Mà V A . B C D = V A . B ' C D ' + V C . B D D ' B '
⇒ V C . B D D ' B ' = V - V 4 = 3 V 4
Đáp án A