Cho hàm số f ( x ) = x 4 - 4 x 2 + 1 Khi đó, phương trình f ( f ( f ( x ) - 1 ) - 2 ) = 1 có bao nhiêu nghiệm thực phân biệt
A. 24
B. 22
C. 26
D. 32
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ở góc trái khung soạn thảo có hỗ trợ viết công thức toán (biểu tượng $\sum$). Bạn viết lại đề bằng cách này để được hỗ trợ tốt hơn.

Bất phương trình m > f(x) - ln(-x) đúng với mọi x ∈ - 1 ; - 1 e
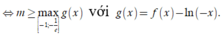
Ta có ![]()
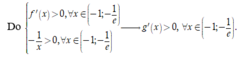
Suy ra hàm số g(x) đồng biến trên ![]()
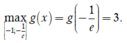
Chọn D.

Chọn B.
Ta có: f(x + 1) = log2(x + 1) và g(x + 2) = log2(2 - x)
![]()
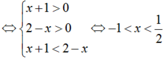

2: ĐKXĐ: x<>1
\(f'\left(x\right)=\dfrac{\left(x^2-3x+3\right)'\left(x-1\right)-\left(x^2-3x+3\right)\left(x-1\right)'}{\left(x-1\right)^2}\)
\(=\dfrac{\left(2x-3\right)\left(x-1\right)-\left(x^2-3x+3\right)}{\left(x-1\right)^2}\)
\(=\dfrac{2x^2-5x+3-x^2+3x-3}{\left(x-1\right)^2}=\dfrac{x^2-2x}{\left(x-1\right)^2}\)
f'(x)=0
=>x^2-2x=0
=>x(x-2)=0
=>\(\left[{}\begin{matrix}x=0\\x=2\end{matrix}\right.\)
1:
\(f\left(x\right)=\dfrac{1}{3}x^3-2\sqrt{2}\cdot x^2+8x-1\)
=>\(f'\left(x\right)=\dfrac{1}{3}\cdot3x^2-2\sqrt{2}\cdot2x+8=x^2-4\sqrt{2}\cdot x+8=\left(x-2\sqrt{2}\right)^2\)
f'(x)=0
=>\(\left(x-2\sqrt{2}\right)^2=0\)
=>\(x-2\sqrt{2}=0\)
=>\(x=2\sqrt{2}\)
Đặt t = f ( f ( x ) - 1 ) - 2 phương trình trở thành:
f ( t ) = 1 ⇔ t 4 - 4 t 2 + 1 = 1 ⇔ t = 0 ; t = ± 2
TH1: Nếu
t = 0 ⇔ f ( f ( x ) - 1 ) - 2 = 0 ⇔ f ( f ( x ) - 1 ) = 2
Đặt a=f(x)-1 phương trình trở thành:
f ( a ) = 2 ⇔ a 4 - 4 a 2 - 1 = 0 ⇔ a = ± 2 + 5
Nhận xét: Xét hàm số y = f ( x ) - 1 = x 4 - 4 x 2 có y c d = y ( 0 ) = 0 ; y c t = y ± 2 = - 4
Với a ∈ - 4 ; 0 phương trình y = a có bốn nghiệm thực phân biệt. Với a = 0 phương trình y = a có hai nghiệm thực phân biệt. Với a < -4 phương trình y = a vô nghiệm.
Áp dụng cho trường này có 2 + 4 = 6 nghiệm.
TH2: Nếu
t = - 2 ⇔ f ( f ( x ) - 1 ) - 2 = - 2 ⇔ f ( f ( x ) - 1 ) = 0
Đặt a=f(x)-1 phương trình trở thành:
f ( a ) = 0 ⇔ a 4 - 4 a 2 + 1 = 0 ⇔ a = ± 2 + 3
Trường hợp này có 2 + 2 + 4 + 4 = 12 nghiệm.
TH3: Nếu t = 2 ↔ f ( f ( x ) - 1 ) = 4 Đặt a=f(x)-1 phương trình trở thành:
f ( a ) = 4 ⇔ a 4 - a = ± 4 a 2 - 3 = 0 ⇔ a = ± 2 + 7
Trường hợp này có 2 + 4 = 6 nghiệm.
Vậy phương trình đã cho có tất cả 24 nghiệm thực phân biệt.
Chọn đáp án A.