Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Đáp án A
HD: Số phần tử của không gian mẫu là n ( Ω ) = C 9 3 . C 6 3 . C 3 3 = 1680
Gọi X là biến cố “ không có phần nào gồm ba viên bi cùng màu”.
Khi đó, ta xét chia thành 3 phần: (2X – 1Đ), (1Đ – 2X), (1Đ – 2X).
Suy ra có C 4 2 . C 5 1 . C 2 1 . C 4 2 . 3 = 1080 cách chọn => n(X) = 1080. Vậy
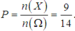
Chọn đáp án A
Vì xác suất không thay đổi khi ta coi ba phần này có xếp thứ tự 1, 2, 3.
Chia ngẫu nhiên 9 viên bi gồm 4 viên màu đỏ và 5 viên màu xanh có cùng kích thước thành 3 phần, mỗi phần 3 viên như sau:
Ø Phần 1: Chọn 3 viên cho phần 1 có C 9 3 cách.
Ø Phần 2: Chọn 3 viên cho phần 2 có C 6 3 cách.
Ø Phần 3: Chọn 3 viên cho phần 3 có 1 cách.
Do đó số phần tử của không gian mẫu là n Ω = C 9 3 . C 6 3 = 1680 .
Gọi A là biến cố không có phần nào gồm 3 viên cùng màu, khi đó ta chia các viên bi thành 3 bộ như sau:
Ø Bộ 1: 2 đỏ, 1 xanh: Có C 4 2 C 5 1 cách chọn.
Ø Bộ 2: 1 đỏ, 2 xanh: Có C 2 1 C 4 2 cách chọn.
Ø Bộ 1: gồm các viên bi còn lại (1 đỏ, 2 xanh) có 1 cách.
Vì bộ 2 và 3 có các viên bi giống nhau để không phân biệt hai bộ này nên có C 3 1 sắp xếp 3 bộ vào 3 phần trên.
Do đó n A = C 4 2 C 5 1 C 2 1 C 4 2 C 3 1 = 1080
Xác suất cần tìm là: P A = n A n Ω = 1080 1680 = 9 14
Đáp án A
Lấy ngẫu nhiên 3 viên bi trong 12 viên bi có
Gọi X là biến cố “3 bi được chọn có đủ 3 màu”
Lấy 1 viên bi màu đỏ trong 3 bi đỏ có 3 cách.
Lấy 1 viên bi màu xanh trong 4 bi xanh có 4 cách.
Lấy 1 viên bi màu vàng trong 5 bi vàng có 5 cách.
Suy ra số kết quả thuận lợi cho biến cố X là
n(X) = 3.4.5 = 60
Đáp án A
Lấy ngẫu nhiên 3 viên bi trong 12 viên bi có C 12 3 = 220 cách ⇒ n Ω = 220 .
Gọi X là biến cố “3 bi được chọn có đủ 3 màu”
Lấy 1 viên bi màu đỏ trong 3 bi đỏ có 3 cách.
Lấy 1 viên bi màu xanh trong 4 bi xanh có 4 cách.
Lấy 1 viên bi màu vàng trong 5 bi vàng có 5 cách.
Suy ra số kết quả thuận lợi cho biến cố X là n X = 3 . 4 . 5 = 60 . Vậy P = n X n Ω = 3 11 .
\(\Omega\) lấy 3 viên bi
\(\left|\Omega\right|=C^3_{12}\)
gọi A" 3 viên lấy ra màu đỏ"
\(\left|A\right|=C^3_7\)
Suy ra
\(P\left(A\right)=\frac{C^3_7}{C^3_{12}}\)
Vì hai túi là khác nhau nên biến cố lấy một viên bi mỗi túi là độc lập.
Gọi biến cố A: “Hai viên bi được lấy có cùng màu xanh”, biến cố B: “Hai viên bi được lấy có cùng màu đỏ”, biến cố C: “Hai viên bi được lấy có cùng màu”
a) Xác suất lấy được viên bi màu xanh từ túi I là \(\frac{3}{{10}}\)
Xác suất lấy được viên bi màu xanh từ túi II là \(\frac{{10}}{{16}} = \frac{5}{8}\)
Xác suất lấy được hai viên bi cùng màu xanh là \(\frac{3}{{10}}.\frac{5}{8} = \frac{3}{{16}}\)
b) Xác suất lấy được viên bi màu đỏ từ túi I là \(\frac{7}{{10}}\)
Xác suất lấy được viên bi màu đỏ từ túi II là \(\frac{6}{{16}} = \frac{3}{8}\)
Xác suất lấy được hai viên bi cùng màu đỏ là \(\frac{7}{{10}}.\frac{3}{8} = \frac{{21}}{{80}}\)
c) Ta có \(C = A \cup B\) mà A và B xung khắc nên
\(P\left( C \right) = P\left( {A \cup B} \right) = P\left( A \right) + P\left( B \right) = \frac{3}{{16}} + \frac{{21}}{{80}} = \frac{9}{{20}}\)
Vậy xác suất để hai viên bi được lấy có cùng màu là \(\frac{9}{{20}}.\)
d) Gọi biến cố D: “Hai viên bi được lấy không cùng màu”
Khi đó \(\overline D = C\)
\( \Rightarrow P\left( D \right) = 1 - P\left( {\overline D } \right) = 1 - P\left( C \right) = 1 - \frac{9}{{20}} = \frac{{11}}{{20}}\)
Vậy xác suất để hai viên bi được lấy không cùng màu là \(\frac{{11}}{{20}}.\)
Đáp án A
Cách 1: Vì xác suất không thay đổi khi ta coi ba phần này có xếp thứ tự 1, 2, 3.
Chia ngẫu nhiên 9 viên bi gồm 4 viên màu đỏ và 5 viên màu xanh có cùng kích thước thành ba phần, mỗi phần 3 viên như sau:
- Phần 1: Chọn 3 viên cho phần 1 có C 9 3
- Phần 2: Chọn 3 viên cho phần 2 có C 6 3 cách.
- Phần 3: Chọn 3 viên cho phần 3 có 1 cách.
Do đó số phần tử của không gian mẫu là
Gọi A là biến cố không có phần nào gồm 3 viên cùng màu, khi đó ta chia các viên bi thành 3 bộ như sau
- Bộ 1: 2 đỏ, 1 xanh: Có C 4 2 C 5 1 cách chọn
- Bộ 2: 1 đỏ, 2 xanh: Có C 2 1 C 4 2 cách chọn
- Bộ 3: gồm các viên bi còn lại (1 đỏ, 2 xanh)
Vì bộ 2 và 3 có các viên bi giống nhau để không phân biệt hai bộ này nên có 3 ! 2 ! sắp xếp 3 bộ vào 3 phần trên. Do đó
Ta được