Đường thẳng y = 1 cắt đồ thị hàm số y = x 3 - 3 x 2 + 2 x + 1 tại ba điểm phân biệt M, N, P biết N nằm giữa M và P. Tính độ dài MP.
A. MP = 2
B. MP = 3
C. MP = 1
D. MP = 4
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Phương trình hoành độ giao điểm
x3+2mx2+3(m-1)x+2 =-x+2 hay x(x2+2mx+3(m-1))=0
suy ra x=0 hoặc x2+2mx+3(m-1)=0 (1)
Đường thẳng d cắt (C) tại ba điểm phân biệt khi và chỉ khi phương trình (1) có hai nghiệm phân biệt khác 0
⇔ m 2 - 3 m + 3 > 0 m - 1 ≠ 0 ⇔ ∀ m m ≠ 1 ⇔ m ≠ 1
Khi đó ta có: C( x1 ; -x1+2) ; B(x2 ; -x2+2) trong đó x1 ; x2 là nghiệm của (1) ; nên theo Viet thì x 1 + x 2 = - 2 m x 1 x 2 = 3 m - 3
Vậy
C B → = ( x 2 - x 1 ; - x 2 + x 1 ) ⇒ C B = 2 ( x 2 - x 1 ) 2 = 8 ( m 2 - 3 m + 3 )
d ( M ; ( d ) ) = - 3 - 1 + 2 2 = 2
Diện tích tam giác MBC bằng khi và chỉ khi
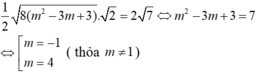
Chọn B.

Vì (1) song song với đường thẳng y=2x+2 nên m+3=2
hay m=-1
Vậy: (1): y=2x+2n-3
Để (1) cắt đường thẳng y=3x-3 tại điểm có hoành độ bằng 2 thì
Thay x=2 vào hàm số y=3x-3, ta được:
\(y=3\cdot2-3=6-3=3\)
Thay x=2 và y=3 vào hàm số y=2x+2n-3, ta được:
\(4+2n-3=3\)
\(\Leftrightarrow2n+1=3\)
\(\Leftrightarrow2n=2\)
hay n=1
Vậy: m=-1 và n=1

Bài 1:
ĐKXĐ:.............
Phương trình hoành độ giao điểm của \((d)\cap (C)\):
\(2(x-m)-\frac{2x-m}{mx+1}=0\Leftrightarrow m(2x^2-2mx-1)=0\)
Nếu \(m=0\Rightarrow (d)\equiv C\) (vô lý) nên $m\neq 0$ . Do đó \(2x^2-2mx-1=0\). $(1)$
Hai điểm $A,B$ có hoành độ chính là nghiệm của phương trình $(1)$
Áp dụng định lý Viet: \(\left\{\begin{matrix} x_1+x_2=m\\ x_1x_2=\frac{-1}{2}\end{matrix}\right.\)
\(d(O,AB)=\frac{|-2m|}{\sqrt{5}}\); \(AB=\sqrt{(x_1-x_)^2+(y_1-y_2)^2}=\sqrt{5(m^2+2)}\)
\(\Rightarrow S_{OAB}=\frac{d(O,AB).AB}{2}=|m|\sqrt{m^2+2}\)
Mặt khác, dễ dàng tính được \(M(m,0),N(0,-2m)\) nên \(S_{OMN}=\frac{OM.ON}{2}=\frac{|m||-2m|}{2}=m^2\)
Ta có \(S_{OAB}=3S_{OMN}\Leftrightarrow |m|\sqrt{m^2+2}=3m^2\)
\(\Rightarrow m=\pm \frac{1}{2}(m\neq 0)\)
Bài 2:
Ta có \(A(1,0,1)\in (d_1);B(3,5,4)\in (d_2); \overrightarrow{u_{d_1}}=(-1,1,1);\overrightarrow{u_{d_2}}=(4,-2,1)\)
Dễ thấy \([\overrightarrow{u_{d_1}},\overrightarrow{u_{d_2}}]\overrightarrow{AB}\neq 0\) nên suy ra $(d_1)$ và $(d_2)$ chéo nhau
Gọi \(\overrightarrow{n_P}\) là vector pháp tuyến của mặt phẳng $(P)$
Khi đó \(\overrightarrow{n_P}=[\overrightarrow{u_{d_1}},\overrightarrow{u_{d_2}}]=(3,5,-2)\)
Vì $(P)$ đi qua $(d_1)$ nên $(P)$ đi qua $A$. Do đó PTMP là:
\(3(x-1)+5y-2(z-1)=0\Leftrightarrow 3x+5y-2z-1=0\)

Xét phương trình hoành độ giao điểm:
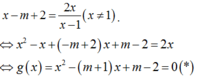
Để đường thẳng d cắt (C) tại 2 điểm phân biệt ⇔ p t * có 2 nghiệm phân biệt khác 1.
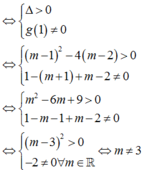
Gọi x A ; x B là 2 nghiệm phân biệt của (*), áp dụng định lí Vi-ét ta có:
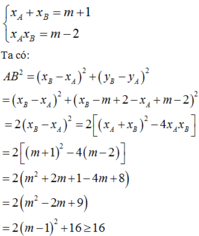
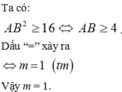
Chọn D.