Cho tam giác ABC có BC = a, BAC ^ = 135 o . Trên đường thẳng vuông góc với (ABC) tại A lấy S thỏa mãn SA = a 2 . Hình chiếu vuông góc của A trên SB, SC lần lượt là M, N. Góc giữa hai mặt phẳng (ABC) và (AMN) là
A. 30 o
B. 45 o
C. 60 o
D. 75 o
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn D
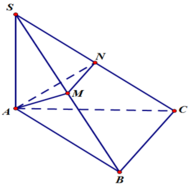
Thể tích khối chóp S. ABC là:
![]()
Do SA=AB=AC=a nên các tam giác SAC, SAB cân tại A.
Theo đề bài M, N là hình chiếu của A trên SB, SC nên M, N lần lượt là trung điểm SB, SC.
Khi đó:
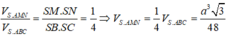
Vậy thể tích khối chóp A. BCNM là:

Chọn B.
Gọi O là tâm đường tròn ngoại tiếp tam giác ABC, và D là điểm đối xứng với A qua O.
Ta có BD ⊥ AB (góc nội tiếp chắn nửa đường tròn).
Và BD ⊥ SA ⇒ BD ⊥ ( SAB ) ⇒ BD ⊥ AM .
Mặt khác AM ⊥ SB ⇒ AM ⊥ ( SBD ) ⇒ SD ⊥ AM .
Chứng minh tương tự ta được SD ⊥ AN ⇒ SD ⊥ ( AMN ) .
Ta có SD ⊥ ( AMN ) SA ⊥ ( ABC ) ⇒ ( ( AMN ) ; ( ABC ) ^ )
= ( SA ; SD ^ ) = ASD ^ .
Ta có: AD = 2 R ABC = BC sin A ^ = a 2
Vậy ( ( AMN ) ; ( ABC ) ^ ) = ASD ^ = arctan 1 = 45 o