Cho hai số phức u, v thỏa mãn u = v = 10 và 3 u - 4 v = 2018 . Tính M = 4 u + 3 v
A. M = 2982
B. M = 50
C. M = 2018
D. M = 482
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
4 tháng 11 2019
Đáp án B
Ta có: u.v =11 nên u.(-v) = -11 (1)
Từ u – v = 10 nên u + (- v) = 10 (2)
Khi đó; u và (-v) là nghiệm phương trình:
x 2 - 10 x - 11 = 0 (*)
Do a - b + c = 1 -(-10 ) + (-11) = 0 nên phương trình (*) có 2 nghiệm là:
x 1 = -1 và x 2 = 11
* Trường hợp 1: Nếu u = -1 và –v = 11
=> v = -11 nên u + v = -12
* Trường hợp 2: nếu u = 11 và –v = -1 thì v = 1
Suy ra: u + v = 12
Trong cả 2 trường hợp ta có: |u + v| = 12
CM
24 tháng 12 2019
Theo giả thiết, ta có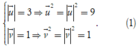 
Từ
u
→
-
v
→
=
4
, suy ra 
Kết hợp (1) và (2) ta được 
Khi đó 
Vậym | u → + v → | = 2
Chọn B.
NT
5
DG
8 tháng 3 2018
Mất 1 tiếng sau khi nhìn cái đề mới giải đc
Ta có \({u+v}≥ 2uv\)
\(=>{(u+v)^2-2uv}≥2uv\)
\(<=>{(u+v)^2/ 2}≥ 2uv\)
Và \({(u+v)^2/4}≥uv\)
\(P= {u^2+v^2}+{33 \over uv}\)
\(≥ {2uv}+{33\over uv}\)
\(={(u+v)^2 \over 2}+{33/{(u+v)^2 \over 4}}\)
Thế số vào ta sẽ đc kết quả \({65 \over 4}\)
Vậy GTNN của P là 65/4 khi u=v = 2
TN
8 tháng 3 2018
Sai!
Ta có \(P=u^2+v^2+\frac{33}{uv}\)
\(\ge\frac{\left(u+v\right)^2}{2}+\frac{33}{\frac{\left(u+v\right)^2}{4}}\)
\(=\frac{4^2}{2}+\frac{33}{\frac{4^2}{4}}=\frac{65}{4}\)
"=" <=> u=v=2
CM
10 tháng 7 2019
Chọn C.
Phương pháp : Chú ý bình phương vô hướng bằng bình phương độ dài.
29 tháng 5 2017
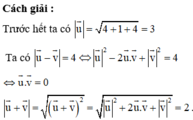
Ta có: \(\hept{\begin{cases}\left(\sqrt{u^2+2}+u\right)\left(\sqrt{u^2+2}-u\right)=2\\\left(\sqrt{v^2-2v+3}+v-1\right)\left(\sqrt{v-2v+3}-v+1\right)=2\end{cases}}\)
Theo đề bài thì ta có:
\(\left(u+\sqrt{u^2+2}\right)\left(v-1+\sqrt{v^2-2v+3}\right)=2\)
Từ đây ta có hệ:
\(\hept{\begin{cases}\sqrt{u^2+2}-u=\sqrt{v^2-2v+3}+v-1\left(1\right)\\\sqrt{u^2+2}+u=\sqrt{v^2-2v+3}-v+1\left(2\right)\end{cases}}\)
Lấy (1) - (2) ta được: \(u+v=1\)
Ta có: \(u^3+v^3+3uv=1\)
\(\Leftrightarrow3uv+u^2-uv+v^2=1\)
\(\Leftrightarrow\left(u+v\right)^2=1\)(đúng)
\(\Rightarrow\)ĐPCM
Đáp án A.