Giải các phương trình sau: 5x – 2 = 0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
11 tháng 3 2022
Đặt x^2 = t ( t > = 0 )
\(2t^2-5t+2=0\)
\(\Delta=25-4.2.2=25-16=9>0\)
Vậy pt có 2 nghiệm pb
\(t=\dfrac{5-3}{4}=\dfrac{1}{2};t=\dfrac{5+3}{4}=2\left(tmđk\right)\)
\(\Rightarrow x=\pm\sqrt{\dfrac{1}{2}}=\pm\dfrac{\sqrt{2}}{2};x=\pm\sqrt{2}\)
11 tháng 3 2022
Đặt \(x^2=y\) ; \(y\ge0\)
Pt trở thành:
\(2y^2-5y+2=0\)
\(\Delta=\left(-5\right)^2-4.2.2=25-16=9\)
\(\Rightarrow\) pt có 2 nghiệm
\(\left\{{}\begin{matrix}y=2\\y=\dfrac{1}{2}\end{matrix}\right.\) (tm)
\(\Leftrightarrow\left\{{}\begin{matrix}x=\pm2\\x=\pm\dfrac{\sqrt{2}}{2}\end{matrix}\right.\)
CM
13 tháng 11 2019
Phương trình bậc hai 3x2 + 5x + 2 = 0
Có a = 3; b = 5; c = 2; Δ = b2 – 4ac = 52 – 4.3.2 = 1 > 0
Áp dụng công thức nghiệm, phương trình có hai nghiệm phân biệt là:
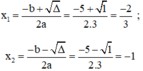
Vậy phương trình có hai nghiệm là -1 và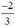 
LM
3
PT
1
CM
26 tháng 3 2017
2 x 2 + 5x + 3 = 0 ⇔ 2 x 2 + 2x + 3x + 3 = 0
⇔ 2x(x + 1) + 3(x + 1) = 0 ⇔ (2x + 3)(x + 1) = 0
⇔ 2x + 3 = 0 hoặc x + 1 = 0
2x + 3 = 0 ⇔ x = -1,5
x + 1 = 0 ⇔ x = -1
Vậy phương trình có nghiệm x = -1,5 hoặc x = -1
PT
1
CM
30 tháng 1 2019
(x – 1)( x 2 + 5x – 2) – ( x 3 – 1) = 0
⇔ (x – 1)( x 2 + 5x – 2) – (x – 1)( x 2 + x + 1) = 0
⇔ (x – 1)[( x 2 + 5x – 2) – ( x 2 + x + 1)] = 0
⇔ (x – 1)( x 2 + 5x – 2 – x 2 – x – 1) = 0
⇔ (x – 1)(4x – 3) = 0 ⇔ x – 1 = 0 hoặc 4x – 3 = 0
x – 1 = 0 ⇔ x = 1
4x – 3 = 0 ⇔ x = 0,75
Vậy phương trình có nghiệm x = 1 hoặc x = 0,75
PT
1
CM
13 tháng 3 2018
b) x 4 - 5 x 2 + 4 = 0
Đặt t = x 2 ≥ 0 , ta có phương trình:
t 2 - 5t + 4 = 0 (dạng a + b + c = 1 -5 + 4 = 0)
t 1 = 1 (nhận) ; t 2 = 4 (nhận)
với t = 1 ⇔ x 2 = 1 ⇔ x = ± 1
với t = 4 ⇔ x 2 = 4 ⇔ x = ± 2
Vậy nghiệm của phương trình x = ±1; x = ± 2
S
23 tháng 2 2021
Mình khuyên bạn thế này :
Bạn nên tách những câu hỏi ra
Như vậy các bạn sẽ dễ giúp
Và cũng có nhiều bạn giúp hơn !
23 tháng 2 2021
Bài 1.
a) ( x - 3 )( x + 7 ) = 0
<=> x - 3 = 0 hoặc x + 7 = 0
<=> x = 3 hoặc x = -7
Vậy S = { 3 ; -7 }
b) ( x - 2 )2 + ( x - 2 )( x - 3 ) = 0
<=> ( x - 2 )( x - 2 + x - 3 ) = 0
<=> ( x - 2 )( 2x - 5 ) = 0
<=> x - 2 = 0 hoặc 2x - 5 = 0
<=> x = 2 hoặc x = 5/2
Vậy S = { 2 ; 5/2 }
c) x2 - 5x + 6 = 0
<=> x2 - 2x - 3x + 6 = 0
<=> x( x - 2 ) - 3( x - 2 ) = 0
<=> ( x - 2 )( x - 3 ) = 0
<=> x - 2 = 0 hoặc x - 3 = 0
<=> x = 2 hoặc x = 3
.
.
QT
1
HQ
Hà Quang Minh
Giáo viên
21 tháng 9 2023
a) \(2\cos x = - \sqrt 2 \Leftrightarrow \cos x = - \frac{{\sqrt 2 }}{2}\;\; \Leftrightarrow \cos x = \cos \frac{\pi }{4} \Leftrightarrow \;\left[ {\begin{array}{*{20}{c}}{x = \frac{\pi }{4} + k2\pi }\\{x = \pi - \frac{\pi }{4} + k2\pi }\end{array}} \right.\;\;\;\;\;\; \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x = \frac{\pi }{4} + k2\pi }\\{x = \frac{{3\pi }}{4} + k2\pi }\end{array}\;\left( {k \in \mathbb{Z}} \right)} \right.\)
b) \(\cos 3x - \sin 5x = 0\;\;\;\; \Leftrightarrow \cos 3x = \sin 5x\;\;\;\; \Leftrightarrow \cos 3x = \cos \left( {\frac{\pi }{2} - 5x} \right)\;\;\)
\( \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{3x = \frac{\pi }{2} - 5x + k2\pi }\\{3x = - \frac{\pi }{2} + 5x + k2\pi }\end{array}} \right.\;\;\;\;\; \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{8x = \frac{\pi }{2} + k2\pi }\\{ - 2x = - \frac{\pi }{2} + k2\pi }\end{array}} \right.\;\; \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x = \frac{\pi }{{16}} + \frac{{k\pi }}{4}}\\{x = \frac{\pi }{4} - k\pi }\end{array}} \right.\;\;\left( {k \in \mathbb{Z}} \right)\)
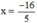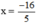5x – 2 = 0 ⇔ 5x = 2 ⇔ x = 2/5