Chứng minh rằng tổng các góc ngoài của một đa giác có số đo bằng 360 0
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



a) Tổng số đo của góc trong và góc ngoài ở mỗi đỉnh của tứ giác (lồi) là 1800 Þ Tổng số đo các góc trong và các góc ngoài của tứ giacs là 4.1800 = 7200.
Mặt khác, tổng số đo các góc trong của tứ giác là: (4-2).1800 = 3600.
Þ Tổng số đo các góc ngoài của tứ giác là: 7200 - 3600 = 3600
Tương tự, ta cũng tính được tổng số đo các góc ngoài của ngũ giác và thập giác là 3600.
b) Tổng số đo của góc trong và góc ngoài ở mỗi đỉnh của hình n - giác (lồi) là 1800 Þ Tổng số đo các góc trong và các góc ngoài của đa giác là n.1800.
Mặt khác, tổng số đo các góc trong của đa giác là (n - 2).1800.
Þ Tổng số đo các góc ngoài của đa giác là:
n.1800 - (n - 2).1800 = 3600.

Chẳng những đối với tam giác mà đối với mọi đa giác lồi,tổng số đo các góc ngoài luôn luôn bằng 360 độ
Ở cuối chương tứ giác (lớp 8),em sẽ học công thức tổng quát tính tổng số đo các góc trong của n-giác lồi (n>=3) là: (n-2).180độ
Góc ngoài tại mỗi đỉnh là góc kề bù với góc trong tại đỉnh đó
Tại n- đỉnh ta có n-góc bẹt là tổng số đo của n-góc TRONG và NGOÀI của n-giác lồi
Vậy tổng số đo n- góc ngoài của n-giác lồi là
n.180độ - (n-2).180độ=2.180độ=360độ
-----------------

Gọi A^1, B^1, C^1 là 3 góc trong của tam giác ABC. A^2, B^2,C^2 là 3 góc ngoài của tam giác ABC.
Ta có:
A^1 + A^2 = 1800
B^1 + B^2 = 1800
C^1 + C^2 = 1800
---------------------
Cộng vế theo vế được:
A^1 +B^1 +C^1 +A^2 +B^2 +C^2 = 3.1800
mà A^1 +B^1 +C^1 = 1800 (tổng 3 góc trong của tam giác)
=> A^2 +B^2 +C^2 = 3.1800 - 1800 = 2.1800 = 3600

Gọi A^1, B^1, C^1 là 3 góc trong của tam giác ABC. A^2, B^2,C^2 là 3 góc ngoài của tam giác ABC.
Ta có: A^1 + A^2 = 180* B^1 + B^2 = 180* C^1 + C^2 = 180*
---------------------
Cộng vế theo vế được: A^1 +B^1 +C^1 +A^2 +B^2 +C^2 = 3.180* mà A^1 +B^1 +C^1 = 180* (tổng 3 góc trong của tam giác)
=> A^2 +B^2 +C^2 = 3.180* - 180* = 2.180* = 360*

Tổng số đo các góc ngoài của đa giác bằng 360 0
Số đo một góc trong của đa giác đều là 468 0 – 360 0 = 108 0
Gọi n là số cạnh của đa giác đều. Ta có số đo mỗi góc của đa giác đều bằng 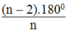
Suy ra: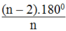 =
108
0
⇒ 180.n – 360 = 108.n⇒ 72n = 360⇒ n = 5
=
108
0
⇒ 180.n – 360 = 108.n⇒ 72n = 360⇒ n = 5
Vậy đa giác đều cần tìm có 5 cạnh.



Tổng số đo của góc trong và góc ngoài ở mỗi đỉnh của hình n-giác bằng 180 0 . Hình n-giác có n đỉnh nên tổng số đo các góc trong và góc ngoài của đa giác bằng n. 180 0 . Mặt khác, ta biết tổng các góc trong của hình n-giác bằng (n – 2). 180 0
Vậy tổng số đo các góc ngoài của hình n-giác là:
n. 180 0 – (n – 2). 180 0 = n. 180 0 – n. 180 0 + 2. 180 0 = 360 0