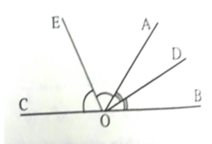
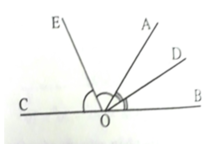
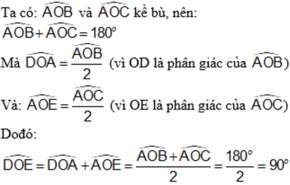Cho 2 góc kề bù A O B ^ và A O C ^ . Hai tia OD, OE lần lượt là 2 tia phân giác của các góc A O B ^ và A O C ^ . Tính số đo góc DOE
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
CM
Cao Minh Tâm
18 tháng 3 2018
Đúng(0)
Những câu hỏi liên quan
13 tháng 4 2020
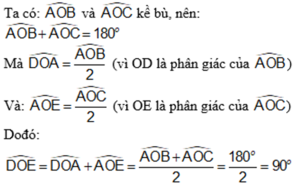
Ủa phải có số đo của mấy góc này cụ thể chứ không có sao mà làm
VC
Vũ Cao Minh⁀ᶦᵈᵒᶫ ( ✎﹏IDΣΛ亗 )
CTV
VIP
13 tháng 4 2020
Vì ^AOB và ^AOC kề bù => ^AOB + ^AOC = 1800 ( 1 )
Có ^DOE = ^AOD + ^AOE do D và E nằm khác nửa mặt phẳng bờ OA ( 2 )
^AOD = ^AOB : 2 do AD là tia phân giác ^AOB ( 3 )
^AOE = ^AOC : 2 do AE là tia phân giác ^AOE ( 4 ). Từ ( 1 )( 2 )( 3 )( 4 )
=> ^DOE = ^AOD + ^AOE = ^AOB : 2 + ^AOC : 2 = ( ^AOB + ^AOC ) : 2
= 1800 : 2 = 900. Vậy ^DOE = 900
23 tháng 4 2017
Theo đề bài cho ta OD và OE là tia phân giác của góc aOb và aOc. Ta sử dụng tính chất góc kề bù bằng 180 độ. Vì nó bằng 180 độ nên ta sử dụng tính chất tia phân giác. Vì có hai tia phân giác nên DOE bằng 180 độ
30 tháng 4 2021
a, Ta có : ∠AOB + ∠BOC = 180o ( Hai góc kề bù ) .
⇒ 80o + ∠BOC = 180o .
⇒ ∠BOC = 180o - 80o .
⇒ ∠BOC = 100o .
Vì tia OD là tia phân giác của ∠AOB nên tia OD nằm giữa hai tia OB và OA và :
∠AOD = ∠DOB = .
=
Vì tia OD nằm giữa hai tia OA và OB mà tia OE nằm trong ∠BOC nên tia OB nằm giữa hai tia OD và OE .
⇒ ∠DOB + ∠BOE = ∠DOE .
⇒ 40o + ∠BOE = 90o ( vì tia OE vuông góc với tia OD nên ∠DOE = 90o ) .
⇒ ∠BOE = 90o - 40o .
⇒ ∠BOE = 50o .
b, Vì tia OE nằm trong ∠BOC nên tia OE nằm giữa hai tia OB avf OC nên :
Ta có : ∠BOE + ∠COE = ∠BOC .
⇒ 50o + ∠COE = 100o .
⇒ ∠COE = 100o - 50o .
⇒ ∠COE = 50o .
Vì ∠BOE = ∠COE và tia OE nằm giữa hai tia OB và OC nên tia OE là tia phân giác của ∠BOC .
Vậy bài toán được chứng minh .
CM
12 tháng 6 2019
a1) Trên nửa mặt phẳng bờ chứa tia AC có: A O B ^ và B O C ^ là 2 góc kề bù mà
Ta có A O B ^ + B O C ^ = A O C ^
⇒ B O C ^ = 180 0 − A O B ^ ⇒ B O C ^ = 100 0
A O B ^ và B O C ^ là hai góc kề bù nên
A O B ^ + B O C ^ = 180 0
⇒
B
O
C
^
=
180
0
−
A
O
B
^
⇒
B
O
C
^
=
100
0
a2) Ta có: OD là tia phân giác của A O B ^ nên A O D ^ = D O B ^ = 80 0 2 = 40 0 .
Ta lại có: Tia OE vuông góc với OD ⇒ O D ⊥ O E ⇒ D O E ^ = 90 0 .
Mà tia OE nằm trong B O C ^ , nên tia OB nằm giữa 2 tia OD và OE.
⇒ D O B ^ + B O E ^ = D O E ^ ⇒ B O E ^ = 90 0 − D O B ^ ⇒ B O E ^ = 50 0
b) Từ đó ta tính được A O E ^ = 130 0 . Mà A O E ^ + E O C ^ = A O C ^ Vì sao
⇒ E O C ^ = 180 0 − A O E ^ ⇒ E O C ^ = 50 0
Vậy tia OE là tia phân giác của B O C ^ .
Tia OE nằm trong B O C ^ nên OE nằm giữa OB và OC.
Suy ra
B O E ^ + E O C ^ = B O C ^
⇒ E O C ^ = B O C ^ − B O E ^ = 100 0 − 50 0 = 50 0
⇒ E O C ^ = E O B ^ (cùng bằng 50 0 ).
Vậy tia OE là tia phân giác của B O C ^ .
30 tháng 7 2018
Bài 4 : * Gọi góc xOz, góc zOy là 2 góc kề bù ; và tia Ou, Ov lần lượt là tia phân giác của góc xOz, zOy.
* Để chứng minh 2 tia phân giác của 2 góc kề bù vuông góc với nhau, ta sẽ chứng minh tia Ou vuông góc tia Ov.
* Vì tia Ou, Ov lần lượt là tia phân giác của góc xOz, zOy
nên:
{ góc uOz = 1/2 góc xOz
{ góc zOv = 1/2 góc zOy
Suy ra:
{ 2 góc uOz = góc xOz
{ 2 góc zOv = góc zOy
Ta lại có:
góc xOz + góc zOy = 180 độ (vì 2 góc xOz, góc zOy kề bù)
=> 2 góc uOz + 2 góc zOv = 180 độ
=> 2(góc uOz + góc zOv) = 180 độ
=> góc uOz + góc zOv = 90 độ
=> góc uOv = 90 độ (vì 2 góc uOz, góc zOv kề nhau)
=> Tia Ou vuông góc Tia Ov
Do đó, 2 tia phân giác của 2 góc kề bù thì vuông góc với nhau. (đpcm)
30 tháng 7 2018
Ta có hình vẽ:
AOBCDE
(vì kí hiệu AOC = BOD = 60o vào hình nhìn hơi rối nên mk ko kí hiệu nx nhé)
a)
- Ta có: AOC + BOC = AOB
=> 60o + BOC = 90o
=> BOC = 90o - 60o = 30o (1)
Lại có: BOC + COD = BOD
=> 30o + COD = 60o
=> COD = 60o - 30o = 30o (2)
Từ (1) và (2) => BOC = COD = 30o => OC là phân giác của BOD
- Ta có: COD + AOD = AOC
=> 30o + AOD = 60o
=> AOD = 60o - 30o = 30o
Vì COD = AOD = 30o nên OD là phân giác của AOC
b) Vì OB là phân giác của DOE nên BOD=BOE=60oBOD=BOE=60o
Ta có: BOC + BOE = COE
=> 30o + 60o = COE
=> COE = 90o
⇒OC⊥OE(đpcm)