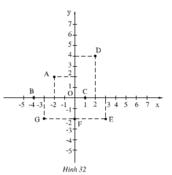
Viết tọa độ điểm A, B, C, D, E, F, G trong hình 32.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
SG
3
18 tháng 4 2017
Ta có tọa độ các điểm: A(-2; 2); B(-4; 0); C(1; 0); D(2; 4); E(3; -2); F(0; -2); G(-3; -2)
RD
3
16 tháng 4 2018
Tọa độ các điểm đó là:
A(-2; 2) ; B(-4; 0)
C(1; 0) ; D(2; 4)
E(3; -2) ; F(0; -2)
G(-3; -2)
PT
1
CM
17 tháng 5 2018
Toạ độ các điểm trong hình vẽ
A(2;-2); B(4;0); C(-2;0); D(2;3); E(2;0); F(-3;2); G(-2;-3)
13 tháng 10 2017
a) Tọa độ các điểm trong hình vẽ là:
A(2;-2); B(4;0); C(-2;0); D(2;3); E(2;0);F(-3;2); G(-2;-3)
b) Ta có hình vẽ ∆ABC:
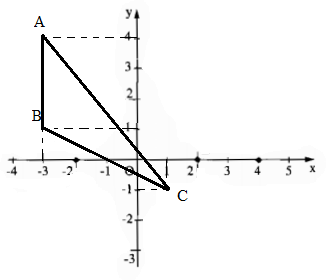
A(-3;4); B(-3;1); C(1;-1).
TA
1 tháng 1 2019
a) Để A B C tạo thành tam giác thì 2 vecto AB à AC phải không cùng phương
Ta có: \(\overrightarrow{AB}=\left(-6;3\right)\)
\(\overrightarrow{AC}=\left(0;-6\right)\)
\(\Rightarrow\) \(\dfrac{-6}{0}\ne\dfrac{3}{-6}\) nên ABC là 1 tam giác
b) G là trọng tâm tam giác ABC:
\(x_G=\dfrac{-4+2+2}{3}=0\) ; \(y_G=\dfrac{1+4+\left(-2\right)}{3}=1\)
\(\Rightarrow\) G(0;1)
c) C là trọng tâm tam giác ABC ?????
d) Làm tương tự như câu a)
Chỉ thay thành dấu "="
e) Để ABCF là hình bình hành thì: \(\overrightarrow{AB}=\overrightarrow{FC}\)
\(\Leftrightarrow\) \(\left(-6;3\right)=\left(2-x_F;-2-y_F\right)\)
\(\Rightarrow\) \(\hept{\begin{cases}2-x_F=-6\\-2-y_F=3\end{cases}}\)\(\Rightarrow\) \(\hept{\begin{cases}x_F=8\\y_F=-5\end{cases}}\)
\(\Rightarrow\) \(F\left(8;-5\right)\)
Tọa độ các điểm đó là:
A(-2; 2) ; B(-4; 0)
C(1; 0) ; D(2; 4)
E(3; -2) ; F(0; -2)
G(-3; -2)