Cho hai đường thẳng chéo nhau d và d’. Đoạn thẳng AB có độ dài bằng a trượt trên d, đoạn thẳng CD có độ dài bằng b trượt trên d’. Chứng minh rằng khối tứ diện ABCD có thể tích không đổi.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
1 tháng 4 2017
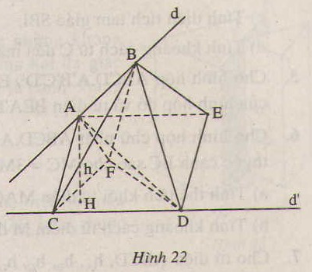
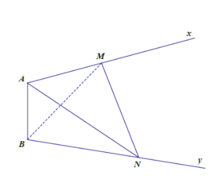
Gọi h là độ dài đường vuông góc chung của d và d’, α là góc giữa hai đường thẳng d và d’. Qua B, A, C dựng hình bình hành BACF. Qua A,C, D dựng hình bình hành ACDE.
Khi đó CFD.ABE là một hình lăng trụ tam giác. Ta có:
VDABC=VDFCB=VBCDF
= VCFD.ABE
= hSFCD=
h.
ab. sinα
=h. ab. sinα (là một số không đổi).
Xem thêm tại: http://loigiaihay.com/cau-6-trang-26-sgk-hinh-hoc-12-c47a2782.html#ixzz4cxsiVwHA
13 tháng 12 2017
a) Trên tia ab, điểm C nằm giữa 2 điểm A và B vì AC<AB (AC=3cm, AB=6cm)
b) Vì C nằm giữa A,B nên AC+CB=AB (AC=3cm, AB=6cm)
3+CB=6
CB=6-3
CB=3
=>CB=3cm
c) C là trung điểm của AB vì:
- C nằm giữa A,B (câu a)
- C cách đều A,B \(AC=CB=\frac{AB}{2}=\frac{6}{2}=3\)
d) Trên tia ab, điểm B nằm giữa C,D vì hai tia đối nhau BC,BD đều chung gốc B và trên cùng đường thẳng
Vì B nằm giữa C,D nên CB + BD= CD (CB=3cm, BD=2cm)
3+2=CD
3+2=5
=>CD=5cm
CM
28 tháng 10 2019
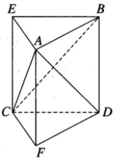
Dựng BE song song và bằng DC, DF song song và bằng BA. Khi đó, ABE.FDC là một lăng trụ đứng.
Ta có:
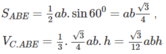
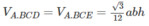
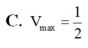
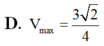
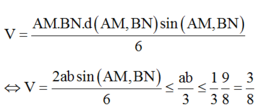
Gọi h là khoảng cách hai đường thẳng d và d’, gọi α là góc tạo bởi hai đường thẳng d và d’.
Lần lượt vẽ hai hình bình hành BACF và ACDE.
Khi đó, ABE.CFD là hình lăng trụ tam tam giác có chiều cao h; AE = CD = b và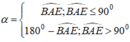
Gọi S là diện tích đáy của hình lăng trụ .
Ta chia hình lăng trụ ABE. CFD thành ba hình chóp tam giác là: D. ABE, B. CFD, D.ABC. Ta có:
Do đó, thể tích khối tứ diện ABCD không đổi.