Tìm tâm và bán kính của các mặt cầu sau đây:
x 2 + y 2 + z 2 – 8x – 2y + 1 = 0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
CM
Cao Minh Tâm
31 tháng 7 2017
Đúng(0)
Những câu hỏi liên quan
26 tháng 5 2017
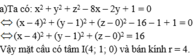
a) Tâm \(I\left(3;-1;8\right)\), bán kính \(r=10\)
b) Tâm \(I\left(-2;1;3\right)\), bán kính \(r=8\)
HT
21 tháng 5 2021
a/ \(x^2-2.4x+16+y^2+2y+1+z^2=16\Leftrightarrow\left(x-4\right)^2+\left(y+1\right)^2+z^2=16\)
\(\Rightarrow\left\{{}\begin{matrix}I\left(4;-1;0\right)\\R=\sqrt{16}=4\end{matrix}\right.\)
b/ \(x^2+y^2+z^2+2x-y+5z-\dfrac{2}{3}=0\Leftrightarrow x^2+2x+1+y^2-2.\dfrac{1}{2}y+\dfrac{1}{4}+z^2+2.\dfrac{5}{2}z+\dfrac{25}{4}=\dfrac{2}{3}+1+\dfrac{1}{4}+\dfrac{25}{4}\)
\(\Leftrightarrow\left(x+1\right)^2+\left(y-\dfrac{1}{2}\right)^2+\left(z+\dfrac{5}{2}\right)^2=\dfrac{49}{6}\) \(\Rightarrow\left\{{}\begin{matrix}I\left(-1;\dfrac{1}{2};-\dfrac{5}{2}\right)\\R=\dfrac{7}{\sqrt{6}}\end{matrix}\right.\)
P/s: câu c bạn tự làm nốt ạ!
CM
4 tháng 3 2019
Đáp án C
Theo công thức tính tâm và bán kính mặt cầu từ phương trình tổng quát, với a = - 1/2, b = 1, c = 0 và d=1 ta có tâm I(1/2;-1;0) và R = 1/2
CM
25 tháng 5 2019
Chọn A
Tìm tâm I và bán kính R của mặt cầu. Tâm J của đường tròn là hình chiếu vuông góc của I trên mặt phẳng α . Bán kính của đường tròn r = R 2 - d 2 với d là khoảng cách từ I đến .