Tìm x từ phương trình 2 + 7 + 12 + ... + x = 245, biết 2, 7, 12, ..., x là cấp số cộng.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

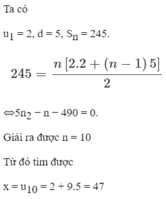

Bài làm
a)dãy số U: \(2,7,12,...x\)
U là cấp số cộng\(\Rightarrow\left\{{}\begin{matrix}d=u_2-u_1=7-2=5\\u_1=2\end{matrix}\right.\)
\(U_n=U_1+\left(n-1\right)d\)
=> \(n=\dfrac{U_n-U_1}{d}+1=\dfrac{x-2}{5}+1=\dfrac{\left(x+3\right)}{5}\)
\(S_n=\dfrac{n\left(U_1+U_n\right)}{2}=\dfrac{\dfrac{\left(x+3\right)}{5}\left(2+x\right)}{2}=\dfrac{\left(x+3\right)\left(x+2\right)}{2.5}=245\)
\(x^2+5x+6=2450\)
\(x^2+5x-2444=0\)
\(\Delta=5^2-4.\left(-2444\right)=9801=\)99^2
\(\left\{{}\begin{matrix}x_1=\dfrac{-5-99}{2}< 0\left(loai\right)\\x_2=\dfrac{-5+99}{2}=47\end{matrix}\right.\)
Đáp số: x=47
b) Xét cấp số cộng 1, 6, 11, ..., 96. Ta có :
\(96=1+\left(n-1\right)5\Rightarrow n=20\)
Suy ra :
\(S_{20}=1+6+11+...+96=\dfrac{20\left(1+96\right)}{2}=970\)
và \(2x.20+970=1010\)
Từ đó : \(x=1\)

Xét cấp số cộng 1, 6, 11, ..., 96.
Ta có: 96 = 1 + 5(n − 1) ⇒ n = 20
Suy ra
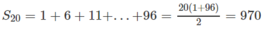
Và 2x.20 + 970 = 1010
Từ đó x = 1

Tìm x thuộc N biết:
X+245=43×11
=>x+245=473
=>x=228
X-382=159:3
=>x-382=53
=>x=53+382=438
7×X+2×X=918
=>(7+2).x=918
=>9x=918
=>x=918:9=102
3×(X-2)+150=240
=>3.(x-2)=240-150
=>3.(x-2)=90
=>x-2=90:3=30
=>x=30+2=32
(X+13):5=12
=>(x+13)=12.5
=>x+13=60
=>x=60-13
=>x=47
Bấm **** nha
360:(X-7)=90
X+245=43*11
X+245=473
x=473-245
X=228
X-382=159:3
X-382=53
X=382+53
X=435
7*X+2*X=918
(7+2)*X=918
9*X=918
X=918:9
X=102
3*(X-2)+150=240
3*(X-2)=240-150
3*(X-2)=90
X-2=90:3
X-2=30
X=30-2
X=28
(X+13):5=12
X+13=12*5
X+13=60
X=60-13
X=47
360:(X-7)=90
X-7=360:90
X-7=4
X=7+4
X=11

\(1)\frac{12}{7}\times \frac{7}{4}+\frac{35}{11}:\frac{245}{121}\)
\(=3+\frac{35}{11}\times \frac{121}{245}\)
\(=3+\frac{11}{7}\)
\(= 3\frac{1}{7}(=\frac{22}{7})\)

Câu 1: Gọi 3 số là a;b;c
\(\Rightarrow\left\{{}\begin{matrix}a+b+c=6\\2b=a+c\\a^2+b^2+c^2=30\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}b=2\\a+c=4\\a^2+c^2=26\end{matrix}\right.\\ \Rightarrow\left\{{}\begin{matrix}b=2\\c=4-a\\a^2+\left(4-a\right)^2=26\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}b=2\\c=5\\a=-1\end{matrix}\right.\left(\text{V\text{ì} }a< c\right)\)
Câu 2: Đặt \(t=x^2\left(t\ge0\right)\)
\(pt:x^4-10\text{x}^2+9m=0\left(1\right)\\ \Leftrightarrow t^2-10t^2+9m=0\left(2\right)\)
Để pt(1) có 4 nghiệm lập thành cấp số cộng thì (2) phải có 2 nghiệm dương phân biệt
\(\)\(\Rightarrow\left\{{}\begin{matrix}\Delta'=\left(-5\right)^2-9m>0\\S=10>0\left(T/m\right)\\P=9m>0\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}m< \dfrac{25}{9}\\\\m>0\end{matrix}\right.\\ \Rightarrow0< m< \dfrac{25}{9}\)
(2) có 2 nghiệm \(t_1< t_2\)
=> (1) có 4 nghiệm \(-\sqrt{t_2}< -\sqrt{t_1}< \sqrt{t_1}< \sqrt{t_2}\)
\(\Rightarrow\sqrt{t_1}=\sqrt{t_2}-\sqrt{t_1}\\ \Rightarrow4t_1=t_2\\ \Rightarrow\left\{{}\begin{matrix}t_1+t_2=10\\4t_1=t_2\\t_1t_2=9m\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}t_1=2\\t_2=8\\m=\dfrac{16}{9}\left(t/m\right)\end{matrix}\right.\)

x2-4x+7 = 0 ⇔ x2 -4x + 4 + 3 = 0
⇔ (x-2)2+3=0 ⇔ (x-2)2=-3 (vô lí)
Vậy pt vô nghiệm
*Chứng minh phương trình \(x^2-4x+7=0\) vô nghiệm
Ta có: \(x^2-4x+7=0\)
\(\Leftrightarrow x^2-4x+4+3=0\)
\(\Leftrightarrow\left(x-2\right)^2+3=0\)
mà \(\left(x-2\right)^2+3\ge3>0\forall x\)
nên \(x\in\varnothing\)(đpcm)

a)
− 12 . x = − 15 . − 4 − 12 − 12 . x = 60 − 12 − 12 . x = 48 x = 48 : − 12 x = − 4
b)
− 9 . x + 3 = − 2 . − 7 + 16 − 9 . x + 3 = 14 + 16 − 9 . x + 3 = 30 − 9 . x = 30 − 3 − 9 . x = 27 x = 27 : − 9 x = − 3
c)
− 12 . x − 34 = 2 − 12 . x = 2 + 34 − 12 . x = 36 x = 36 : − 12 x = − 3

a)
− 12 . x = − 15 . − 4 − 12 − 12 . x = 60 − 12 − 12 . x = 48 x = 48 : − 12 x = − 4
b)
− 9 . x + 3 = − 2 . − 7 + 16 − 9 . x + 3 = 14 + 16 − 9 . x + 3 = 30 − 9 . x = 30 − 3 − 9 . x = 27 x = 27 : − 9 x = − 3
c)
− 12 . x − 34 = 2 − 12 . x = 2 + 34 − 12 . x = 36 x = 36 : − 12 x = − 3

\(ac=-12< 0\) nên pt luôn có 2 nghiệm pb trái dấu
Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=2\left(m+1\right)\\x_1x_2=-12\end{matrix}\right.\)
\(x_1^2-x_2^2-14\left(m+1\right)=0\)
\(\Leftrightarrow\left(x_1-x_2\right)\left(x_1+x_2\right)-14\left(m+1\right)=0\)
\(\Leftrightarrow\left(x_1-x_2\right).2\left(m+1\right)-14\left(m+1\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}m=-1\\x_1-x_2=7\left(1\right)\end{matrix}\right.\)
Xét (1), kết hợp với Viet ta được: \(\left\{{}\begin{matrix}x_1+x_2=2\left(m+1\right)\\x_1-x_2=7\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}x_1=\dfrac{2m+9}{2}\\x_2=\dfrac{2m-5}{2}\end{matrix}\right.\)
Thế vào \(x_1x_2=-12\Leftrightarrow\left(\dfrac{2m+9}{2}\right)\left(\dfrac{2m-5}{2}\right)=-12\)
\(\Leftrightarrow4m^2+8m+3=0\Rightarrow\left[{}\begin{matrix}m=-\dfrac{3}{2}\\m=-\dfrac{1}{2}\end{matrix}\right.\)
Vậy \(m=\left\{-1;-\dfrac{3}{2};-\dfrac{1}{2}\right\}\)