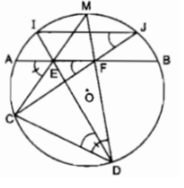
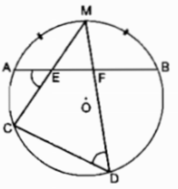
Cho đường tròn tâm O bán kính R và dây AB bất kỳ. Gọi M là điểm chính giữa của cung nhỏ AB. E và F là hai điểm bất kỳ trên dây AB. Gọi C và D tương ứng là giao điểm của ME, MF của đường tròn (O). Chứng minh ∠ EFD + ∠ ECD = 180 °
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

CM
Cao Minh Tâm
3 tháng 7 2018

Đúng(0)
Những câu hỏi liên quan

30 tháng 6 2023
a: Xét ΔAFC và ΔBEC có
CA=CB
góc CAF=góc CBE
AF=BE
=>ΔAFC=ΔBEC
b: góc FCA=góc ECB
góc ACB=90 độ
=>góc ACE+góc BCE=90 độ
=>góc FCA+góc ACE=90 độ
=>góc FCE=90 độ
mà góc CFE=1/2*sđ cung CB=45 độ
nên ΔCFE vuông cân tại C

1 tháng 7 2023
a: C là điểm chính giữa của cung AB
=>OC vuông góc AB tại I
=>CD là đường kính của (O)
góc CMD=1/2*sđ cung CD=90 độ
góc EMD+góc EID=180 độ
=>EMDI nội tiếp
b: Xét ΔCBE và ΔCMB có
góc BCE chung
góc CBE=góc CMB
=>ΔCBE đồng dạng với ΔCMB
=>CB/CM=CE/CB
=>CB^2=CM*CE
=>góc CBE=góc CMB
=>CB là tiếp tuyến của đường tròn ngoại tiếp ΔBME