Chứng minh các đẳng thức sau: x 6 x + 2 x 3 + 6 x : 6 x = 2 1 3 v ớ i x > 0
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) a) Biến đổi vế trái thành 32√6+23√6−42√6326+236−426 và làm tiếp.
b) Biến đổi vế trái thành (√6x+13√6x+√6x):√6x(6x+136x+6x):6x và làm tiếp



a) Biến đổi vế trái ta có:
\(\frac{3}{2}\sqrt{6}+2\sqrt{\frac{2}{3}}-4\sqrt{\frac{3}{2}}\)
\(=\frac{3\sqrt{6}}{2}+\frac{2\sqrt{6}}{3}-\frac{4\sqrt{6}}{2}=\frac{9\sqrt{6}+4\sqrt{6}-12\sqrt{6}}{6}=\frac{\sqrt{6}}{6}=VP\)
Vậy đẳng thức trên đc chứng minh
b) Biến đổi vế trái ta có:
\(\left(x\sqrt{\frac{6}{x}}+\sqrt{\frac{2x}{3}}+\sqrt{6x}\right):\sqrt{6x}\)
\(=\left(x\sqrt{\frac{6}{x}}+\sqrt{\frac{2x}{3}}+\sqrt{6x}\right)\cdot\frac{1}{\sqrt{6x}}\)
\(=x\sqrt{\frac{6}{x}\cdot\frac{1}{6x}}+\sqrt{\frac{2x}{3}\cdot\frac{1}{6x}}+\sqrt{6x}\cdot\frac{1}{\sqrt{6x}}\)
\(=x\sqrt{\frac{1}{x^2}}+\sqrt{\frac{1}{9}}+1=1+\frac{1}{3}+1=2\frac{1}{3}=VP\)
Vậy đẳng thức trên đc chứng minh

1 ) \(x^2+x+1=x^2+x+\dfrac{1}{4}+\dfrac{3}{4}=\left(x+\dfrac{1}{2}\right)^2+\dfrac{3}{4}\ge\dfrac{3}{4}>0\forall x\left(đpcm\right)\)
2 ) \(x^2+3x+3=x^2+3x+\dfrac{9}{4}+\dfrac{3}{4}=\left(x+\dfrac{3}{2}\right)^2+\dfrac{3}{4}\ge\dfrac{3}{4}>0\forall x\left(đpcm\right)\)
3 ) \(x^2+y^2+2\left(x-2y\right)+6\)
\(=x^2+y^2+2x-4y+6\)
\(=\left(x^2+2x+1\right)+\left(y^2-4y+4\right)+1\)
\(=\left(x+1\right)^2+\left(y-2\right)^2+1\ge1>0\forall x\left(đpcm\right)\)
1) x2 +x+1
= (x2 +2.x.1/2 +1/4) +3/4
= (x+1/2)2+3/4 \(\ge\dfrac{3}{4}\forall x\in R\left(Vì:\left(x+\dfrac{1}{2}\right)^2\ge0\forall x\in R\right)\)
2) x2 + 3x+3
= (x2 +2.x.3/2 + 9/4)+ 3/4
= ( x+ 3/2)2 + 3/4 \(\ge\dfrac{3}{4}\forall x\in R\left(Vì:\left(x+\dfrac{3}{2}\right)^2\ge0\forall x\in R\right)\)

a: \(VT=\dfrac{3\sqrt{6}}{2}+\dfrac{2\sqrt{6}}{3}-\dfrac{4\sqrt{6}}{2}\)
\(=\dfrac{-\sqrt{6}}{2}+\dfrac{2\sqrt{6}}{3}=\dfrac{-3\sqrt{6}+4\sqrt{6}}{6}=\dfrac{\sqrt{6}}{6}\)
b: \(VT=\dfrac{\left(\sqrt{6x}+\dfrac{\sqrt{6x}}{3}+\sqrt{6x}\right)}{\sqrt{6x}}\)
\(=1+\dfrac{1}{3}+1=2\dfrac{1}{3}\)
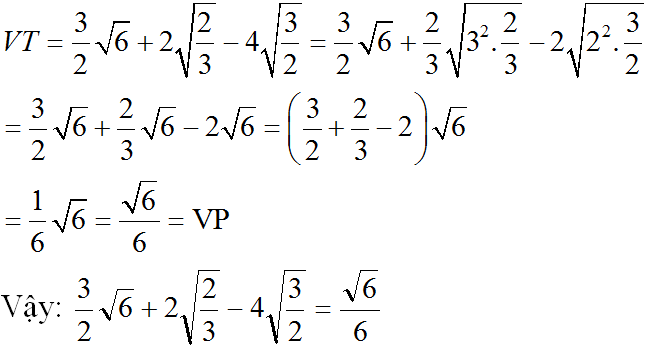
Biến đổi vế trái: