Cho góc α thỏa mãn 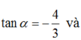
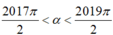 . Tính sinα
. Tính sinα
![]()
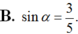
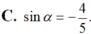
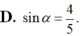
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Chọn A.
Ta có 3cosα+ 2sinα = 2 hay (3cosα+ 2sinα = 2 )2 = 4
Tương đương: 9 cos2 α + 12 cosα .sin α + 4sin2α = 4
Hay 5cos2α + 12 cosα .sin α = 0
Từ đó: cosα= 0 hoặc 5cosα + 12 sinα = 0
+ Nếu cosα = 0 thì sinα =1: loại ( vì sinα < 0).
+ 5cosα + 12 sinα = 0
ta có hệ phương trình 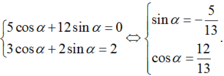

Chọn A.
Ta có : P = sin3 α + cos3 α = ( sinα + cosα) 3 - 3sin α.cosα(sinα + cosα)
Ta có (sin α + cos α) 2 = sin2α + cos2α + 2sinα.cosα = 1 + 24/25 = 49/25.
Vì sin α + cosα > 0 nên ta chọn sinα + cosα = 7/5.
Thay 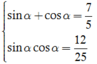 vào P ta được
vào P ta được 

Chọn D.
Ta có ( sinα - cosα) 2 + (sinα + cosα) 2 = 2( sin2α + cos2α) = 2.
Suy ra (sinα - cosα) 2 = 2 - ( sinα + cos α) 2 = 2 - 5/4 = 3/4.
Do ![]() suy ra sinα < cosα nên sinα - cosα < 0.
suy ra sinα < cosα nên sinα - cosα < 0.
Vậy 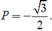
Chọn D.
Ta có
Mà