Tính diện tích toàn phần S của hình chóp có đáy là hình vuông diện tích bằng 4 và các mặt bên là các tam giác đều.
A. S = 4
B. S = 4 + 3
C. S = 4 + 4 3
D. S = 4 + 4 2
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

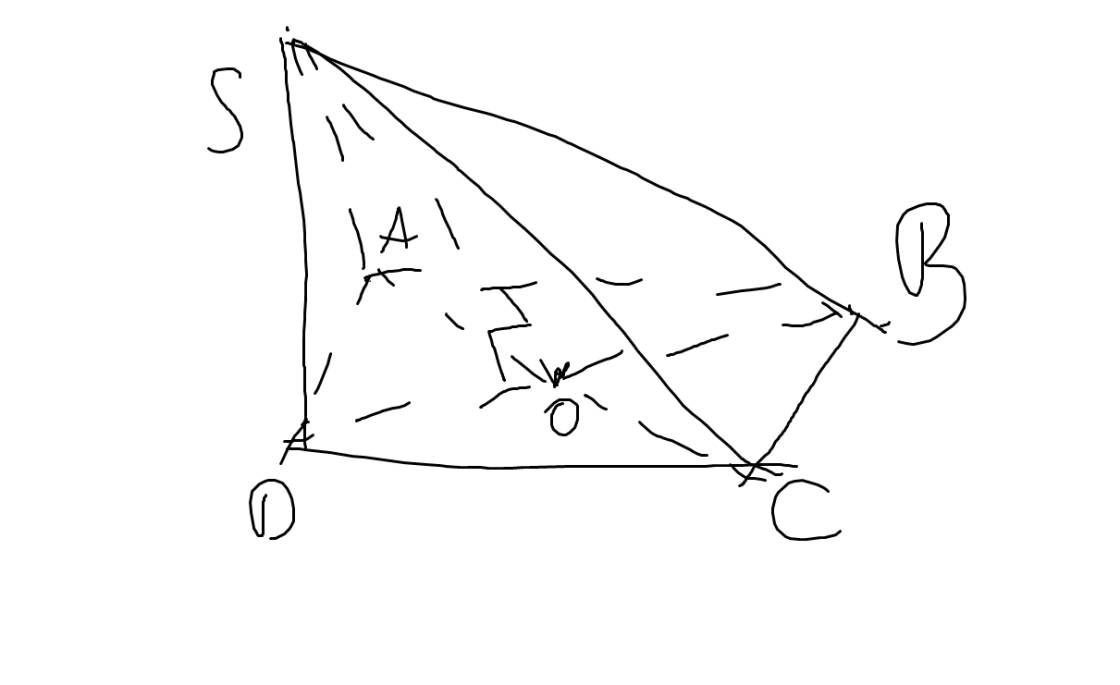
Trong hình chóp tứ giác đều, đường cao kẻ từ đỉnh xuống đáy có chân đường cao là tâm của đáy và đường cao đó chính là trung đoạn của hình chóp
a: Vẽ SO\(\perp\)(ABCD)
=>SO là trung đoạn của hình chóp ABCD và O là tâm của hình vuông ABCD
=>O là trung điểm chung của AC và BD
ABCD là hình vuông
=>\(AC=BD=\sqrt{4^2+4^2}=4\sqrt{2}\left(cm\right)\)
=>\(AO=BO=CO=DO=\dfrac{4\sqrt{2}}{2}=2\sqrt{2}\left(cm\right)\)
SO vuông góc (ABCD)
=>SO vuông góc OD
=>ΔSOD vuông tại O
=>\(SO^2+OD^2=SD^2\)
=>\(SO^2=6^2-8=28\)
=>\(SO=2\sqrt{7}\left(cm\right)\)
b: \(S_{Xq}=p\cdot d=C_{đáy}\cdot SO=4\cdot4\cdot2\sqrt{7}=32\sqrt{7}\left(cm^2\right)\)
c: \(S_{tp}=S_{xq}+S_{đáy}\)
\(=32\sqrt{7}+4^2=32\sqrt{7}+16\left(cm^2\right)\)

Đáp án là C
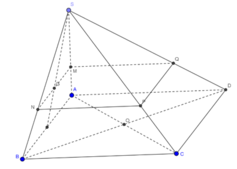
Cách 1. Ta có mặt phẳng (P) đi qua trọng tâm của tam giác SAB cắt các cạnh của khối chóp lần lượt tại M, N, P, Q. Với MN//AB, NP//BC, PQ//CD, QM//AD.
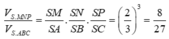
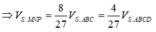
Tương tự 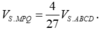
Nên 
Đặt AB = x.
Ta có 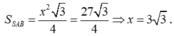
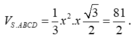
Từ đó 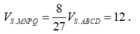
Cách 2. Do hai khối chóp S.MNPQ, S.ABCD đồng dạng với nhau theo tỉ số k = 2 3 nên tỉ lệ thể tích là
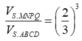
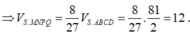

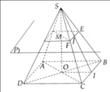
a) Gọi O là tâm của đáy ABCD, M là giao điểm của SO và mặt phẳng (P). Ta có: OM = 2(cm).
Ta tính được O B = 2 2 c m rồi suy ra SO = 5 (cm)
Từ đó chiều cao cần tìm là: SM = SO - OM 3 (cm)
b) Gọi I là trung điểm của BC. E, F, J lần lượt là giao điểm của SB, SC, SI với mặt phẳng (p).
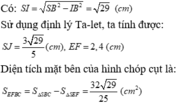

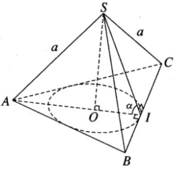
Gọi I là trung điểm của cạnh BC và O là tâm của tam giác đều ABC. Theo giả thiết ta có SA = SB = SC = a và ∠ SIO = α. Đặt OI = r, SO = h, ta có AO = 2r và

Do đó a 2 = r 2 tan 2 α + 4 r 2 = r 2 tan 2 α + 4
Vậy 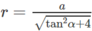
Hình nón nội tiếp có đường sinh là :
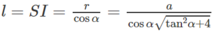
Diện tích xung quanh của hình nón nội tiếp hình chóp S.ABC là:
![]()
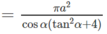
Đáp án C
Cạnh đáy của hình chóp bằng 2 và diện tích một mặt bên bằng nên 2 2 3 4 = 3 nên S t p = 4 + 4 3