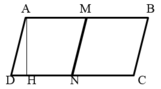
Cho hình bình hành ABCD có M và N là trung điểm của AB và CD. Biết DN = 18 cm, AH = 22 cm (như hình vẽ ): Tính tổng diện tích của các hình bình hành có trong hình vẽ :
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
21 tháng 2 2022
Nếu không trả lời đầy đủ em bảo chị làm bài giải luôn cho dễ hiểu nhé
13 tháng 3 2022
(có nhiều cách giải)
Hình bên có tất cả 3 hình nình hành gồm AMND, MBCN và ABCD
Vì M và N là trung điểm của AB và CD nên AM = MB = DN = Nc = 18 cm
Diện tích hình bình hành AMND là : 22 x 18 = 369 (cm2)
Tổng diện tích các hình bình hành có trong hình vẽ chính bằng tổng diện tích của 4 hình bình hành AMND là : 396 x 4 = 1584 cm2
Đáp số : 1584 cm2
DM
7 tháng 2 2021
a, \(S_{ABCD}\) = AH.CD
= 3.4
= 12 (\(cm^2\))
b, Ta có M là trung điểm AB
⇒ AM = \(\dfrac{AB}{2}\) = \(\dfrac{4}{2}\) = 2 (cm)
\(S_{ADM}\) = \(\dfrac{AH.AM}{2}\)
= \(\dfrac{3.2}{2}\)
= 3 (\(cm^2\))
c, Gọi O là trung điểm
DM
7 tháng 2 2021
c, Gọi O là trung điểm ND
Từ O kẻ OP // CD
Xét ΔNDC có: NO = OD
OP // CD
⇒ OP là đường trung bình ΔNDC
⇒ OP = \(\dfrac{1}{2}DC\) mà DC = 4 cm
⇒ OP = 2 cm
Xét ΔAMN và ΔPON có:
Góc BAC = góc APO
Góc MOP = góc AMD
AM = ON
⇒ ΔAMN = ΔPON (g.c.g)
⇒ NM = ON mà ON = \(\dfrac{1}{2}DM\)
⇒ DN = 2MN
31 tháng 1 2021
a) Gọi H là chân đường vuông góc kẻ từ A xuống CD
Theo đề bài, ta có: AH=3(cm)
Xét hình bình hành ABCD có AH là đường cao ứng với cạnh CD(gt)
nên \(S_{ABCD}=AH\cdot CD=4\cdot3=12\left(cm^2\right)\)
(có nhiều cách giải)
Hình bên có tất cả 3 hình nình hành gồm AMND, MBCN và ABCD
Vì M và N là trung điểm của AB và CD nên AM = MB = DN = Nc = 18 cm
Diện tích hình bình hành AMND là : 22 x 18 = 369 (cm2)
Tổng diện tích các hình bình hành có trong hình vẽ chính bằng tổng diện tích của 4 hình bình hành AMND là : 396 x 4 = 1584 cm2
Đáp số : 1584 cm2
ĐÚNG 100%100