Tìm X:
b) X + 31 10 = 14,5 + 12 10
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
CM
Cao Minh Tâm
28 tháng 10 2017
Đúng(0)
Những câu hỏi liên quan
S
6
16 tháng 7 2018
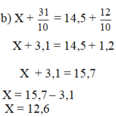
\(x+\frac{31}{10}=14,5+\frac{12}{10}\)
\(x+\frac{31}{10}=\frac{29}{2}+\frac{12}{10}\)
\(x+\frac{31}{10}=\frac{157}{10}\)
\(x=\frac{157}{10}-\frac{31}{10}\)
\(x=\frac{63}{5}\)
Học tốt #
16 tháng 7 2018
\(x+\frac{31}{10}=14,5+\frac{12}{10}\)
\(\Rightarrow x+\frac{31}{10}=\frac{157}{10}\)
\(\Rightarrow x=\frac{157}{10}-\frac{31}{10}\)
\(\Rightarrow x=\frac{63}{5}\)
Vậy \(x=\frac{63}{5}\)
_Chúc bạn học tốt_
DN
19 tháng 4 2018
\(x+\frac{31}{10}=x+\frac{12}{10}+\frac{19}{10}=14,5+\frac{12}{10}\)
\(x+\frac{19}{10}=14,5\)
\(x+1,9=14,5\)
\(x=14,5-1,9=12,6\)
19 tháng 4 2018
x+\(\frac{31}{10}\)=\(\frac{157}{10}\)
x=\(\frac{157}{10}-\frac{31}{10}\)
x=\(\frac{63}{5}\)
1 tháng 5 2019
a)Ta có :
x-8,7=5 x 1,2 = 6
=> x = 6+8,7 = 14,7
Vậy x=14,7
b) Ta có
x+31/10=14,5+12/10=15,7
=> x=15,7-31/10=12,6.
Vậy x=12,6
2 tháng 5 2019
a) ( x - 8,7 ) = 5 * 1,2
x - 8,7 = 6
x = 6 + 8,7
x = 14,7
b) x + 31/10 = 14,5 +12/10
NY
5
18 tháng 10 2021
\(b,\Rightarrow x+1-4⋮x+1\\ \Rightarrow x+1\inƯ\left(4\right)=\left\{-4;-2;-1;1;2;4\right\}\\ \Rightarrow x\in\left\{-5;-3;-2;0;1;3\right\}\\ c,\Rightarrow3\left(2x+1\right)-2\left(3x-2\right)⋮3x-2\\ \Rightarrow6x+3-6x+4⋮3x-2\\ \Rightarrow7⋮3x-2\\ \Rightarrow3x-2\inƯ\left(7\right)=\left\{-7;-1;1;7\right\}\\ \Rightarrow x\in\left\{-\dfrac{5}{3};\dfrac{1}{3}1;3\right\}\)
NH
2
3 tháng 4 2021
Ta có: \(2^x=\dfrac{1}{4}\cdot\dfrac{2}{6}\cdot\dfrac{3}{8}\cdot\dfrac{4}{10}\cdot\dfrac{5}{12}\cdot...\cdot\dfrac{30}{62}\cdot\dfrac{31}{64}\)
\(\Leftrightarrow2^x=\dfrac{1\cdot2\cdot3\cdot4\cdot...\cdot31}{2\cdot\left(2\cdot3\cdot4\cdot...\cdot31\right)\cdot64}\)
\(\Leftrightarrow2^x=\dfrac{1}{2}\cdot\dfrac{1}{64}=\dfrac{1}{128}\)
\(\Leftrightarrow2^x=\dfrac{1}{2^6}\)
\(\Leftrightarrow2^{x+6}=1\)
\(\Leftrightarrow x+6=0\)
hay x=-6
Vậy: x=-6
TA
3 tháng 4 2021
`1/4 . 2/6 . 3/8 ... . 30/62 .31/64 =2^x`
`-> (1.2.3....30.31)/(4.6.8....62.64)=2^x`
`-> (1.(2.3...31))/(2.(2.3.4...31).32)=2^x`
`-> 1/(2.32)=2^x`
`-> 1/64=2^x`
`-> 1/(2^6)=2^x`
`-> x=-6`.
NT
1
2 tháng 4 2017
Có: \(\frac{1}{4}.\frac{2}{6}.\frac{3}{8}.\frac{4}{10}...\frac{30}{62}.\frac{31}{64}=\frac{1}{2.2}.\frac{2}{2.3}.\frac{3}{2.4}...\frac{30}{2.31}.\frac{31}{2.32}=\frac{1}{2}.\frac{1}{2}.\frac{1}{2}...\frac{1}{2}.\frac{1}{2}.\frac{1}{32}\)
\(=\frac{1}{2^{31}.2^5}=\frac{1}{2^{36}}=2^x\)\(\Rightarrow1=2^x.2^{36}=2^{36+x}\)\(\Rightarrow2^{36+x}=2^0\Rightarrow36+x=0\Rightarrow x=-36\)