Cho tam giác ABC vuông tại A, đường cao AH. Trên tia BC lấy điểm D sao cho BD = BA. Đường vuông góc với BC tại D cắt AC tại E, cắt BA tại F. Chứng minh
c. Tia BE là tia phân giác của (ABC)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
24 tháng 5 2019
A.Xét ΔABE và ΔDBE có:
Cạnh BE chung
BD = BA
⇒ ΔABE = ΔDBE (cạnh huyền – góc nhọn)
b. Do BD = BA nên B nằm trên đường trung trực của AD
Do ΔABE = ΔDBE ⇒ AE = ED (hai cạnh tương ứng)
E nằm trên đường trung trực của AD
Vậy BE là đường trung trực của AD
c. Do ΔABE = ΔDBE ⇒ ∠(ABE) = ∠(EBC) (hai góc tương ứng)
Suy ra BE là tia phân giác của góc ABC
CM
24 tháng 1 2018
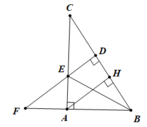
b. Do BD = BA nên B nằm trên đường trung trực của AD
Do ΔABE = ΔDBE ⇒ AE = ED (hai cạnh tương ứng) (1 điểm)
E nằm trên đường trung trực của AD (1 điểm)
Vậy BE là đường trung trực của AD (0.5 điểm)
CM
12 tháng 1 2017
a. Hình vẽ (0.5 điểm)
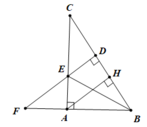
Xét ΔABE và ΔDBE có:
Cạnh BE chung
BD = BA
⇒ ΔABE = ΔDBE (cạnh huyền – góc nhọn) (1 điểm)
10 tháng 5 2023
a: Xét ΔBAE vuông tại A và ΔBDE vuông tại D có
BE chung
BA=BD
=>ΔBAE=ΔBDE
b; BA=BD
EA=ED
=>BE là trung trực của AD
28 tháng 5 2020
Bài làm
a) Xét tam ABC vuông tại A có:
\(\widehat{ACB}+\widehat{ABC}=90^0\)( hai góc phụ nhau )
hay \(\widehat{ACB}+60^0=90^0\)
=> \(\widehat{ACB}=90^0-60^0=30^0\)
b) Xét tam giác ABE và tam giác DBE có:
\(\widehat{BAE}=\widehat{BDE}=90^0\)
Cạnh huyền: BE chung
Cạnh góc vuông: AB = BD ( gt )
=> Tam giác ABE = tam giác DBE ( cạnh huyền - cạnh góc vuông )
=> \(\widehat{ABE}=\widehat{DBE}\)( hai góc tương ứng )
=> BI là tia phân giác của góc BAC
Mà I thược BE
=> BE là tia phân giác của góc BAC
Gọi I là giao điểm BE và AD
Xét tam giác AIB và tam giác DIB có:
AB = BD ( gt )
\(\widehat{ABE}=\widehat{DBE}\)( cmt )
BI chung
=> Tam giác AIB = tam giác DIB ( c.g.c )
=> AI = ID (1)
=> \(\widehat{BIA}=\widehat{BID}\)
Ta có: \(\widehat{BIA}+\widehat{BID}=180^0\)( hai góc kề bù )
Hay \(\widehat{BIA}=\widehat{BID}=\frac{180^0}{2}=90^0\)
=> BI vuông góc với AD tại I (2)
Từ (1) và (2) => BI là đường trung trực của đoạn AD
Mà I thược BE
=> BE là đường trung trực của đoạn AD ( đpcm )
c) Vì tam giác ABE = tam giác DBE ( cmt )
=> AE = ED ( hai cạnh tương ứng )
Xét tam giác AEF và tam giác DEC có:
\(\widehat{EAF}=\widehat{EDC}=90^0\)
AE = ED ( cmt )
\(\widehat{AEF}=\widehat{DEF}\)( hai góc đối )
=> Tam giác AEF = tam giác DEC ( g.c.g )
=> AF = DC
Ta có: AF + AB = BF
DC + BD = BC
Mà AF = DC ( cmt )
AB = BD ( gt )
=> BF = BC
=> Tam giác BFC cân tại B
=> \(\widehat{BFC}=\widehat{BCF}=\frac{180^0-\widehat{FBC}}{2}\) (3)
Vì tam giác BAD cân tại B ( cmt )
=> \(\widehat{BAD}=\widehat{BDA}=\frac{180^0-\widehat{FBC}}{2}\) (4)
Từ (3) và (4) => \(\widehat{BAD}=\widehat{BFC}\)
Mà Hai góc này ở vị trí đồng vị
=> AD // FC
d) Xét tam giác ABC vuông tại A có:
\(\widehat{ACB}+\widehat{ABC}=90^0\)( hai góc phụ nhau ) (5)
Xét tam giác DEC vuông tại D có:
\(\widehat{DEC}+\widehat{ACB}=90^0\)( hai góc phụ nhau ) (6)
Từ (5) và (6) => \(\widehat{ABC}=\widehat{DEC}\)
Ta lại có:
\(\widehat{ABC}>\widehat{EBC}\)
=> AC > EC
Mà \(\widehat{EBC}=\frac{1}{2}\widehat{ABC}\)
=> EC = 1/2 AC.
=> E là trung điểm AC
Mà EC = EF ( do tam giác AEF = tam giác EDC )
=> EF = 1/2AC
=> AE = EC = EF
Và AE = ED ( cmt )
=> ED = EC
Mà EC = 1/2AC ( cmt )
=> ED = 1/2AC
=> 2ED = AC ( đpcm )
Mình chứng minh ra kiểu này cơ. không biết đề đúng hay sai!??
23 tháng 7 2023
a: AH<AD
=>H nằm giữa B và D
b: Xét ΔBAE vuông tại A và ΔBDE vuông tại D có
BE chung
BA=BD
=>ΔBAE=ΔBDE
=>EA=ED
mà BA=BD
nên BE là trung trực của AD
c: góc CAD+góc BAD=90 độ
góc HAD+góc BDA=90 độ
mà góc BAD=góc BDA
nên góc CAD=góc HAD
=>AD là phân giác của góc HAC
c. Do ΔABE = ΔDBE ⇒ ∠(ABE) = ∠(EBC) (hai góc tương ứng)
Suy ra BE là tia phân giác của góc ABC (1 điểm)