Một hình chóp tứ giác đều S.ABCD có cạnh bên SA = 13cm và độ dài cạnh đáy là 5 2 . Tính thể tích của hình chóp tứ giác đều.
A. 200 c m 3
B. 150 c m 3
C. 180 c m 3
D. 210 c m 3
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) Ta có: AC2 = AB2 + BC2 (Pytago) = 32 + 32 = 18(cm)
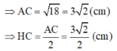
Lại có: SH2 = SC2 - HC2 (Pytago)
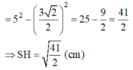
b) Gọi K là trung điểm của BC
Ta có: SK2 = SH2 + HK2 (Pytago)
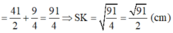
![]()
![]()
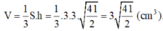

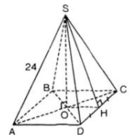
a) S.ABCD là hình chóp tứ giác đều
⇒ ABCD là hình vuông
⇒ AC = AB√2 = 20√2 (cm).
SO là chiều cao của hình chóp
⇒ O = AC ∩ BD và SO ⊥ (ABCD)
⇒ SO ⊥ AO
⇒ ΔSAO vuông tại O
⇒ SO2 + OA2 = SA2
⇒ SO2 = SA2 – OA2 = SA2 – (AC/2)2 = 242 - 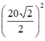 = 376
= 376
⇒ SO = √376 ≈ 19,4 (cm).
Thể tích hình chóp:
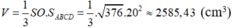
b) Gọi H là trung điểm của CD
SH2 = SD2 – DH2 = 242 – 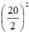 = 476
= 476
⇒ SH = √476 ≈ 21,8 (cm)
⇒ Sxq = p.d = 2.AB.SH = 2.20.√476 ≈ 872,7 (cm2 ).
Sđ = AB2 = 202 = 400 (cm2 )
⇒ Stp = Sxq + Sđ = 872,7 + 400 = 1272,7 (cm2 ).

\(V_{chóp.tứ.giác.đêu}=\dfrac{1}{3}.S_{đáy}.h\\ \Leftrightarrow400=\dfrac{1}{3}.a^2.h=\dfrac{1}{3}.10^2.h\\ \Leftrightarrow h=\dfrac{400\times3}{10^2}=12\left(mm\right)\)

a) Áp dụng định lý Pytago, ta được:
AC2=AB2+BC2=2AB2AC2=AB2+BC2=2AB2
⇒AC=AB√2=10√2cm⇒AC=AB2=102cm
b) Gọi MM là trung điểm ABAB
⇒MA=MB=MO=5cm⇒MA=MB=MO=5cm
⇒SM⊥AB⇒SM⊥AB (ΔSAB∆SAB cân tại SS)
⇒SM=√SA2−AM2=√122−52=√119cm⇒SM=SA2−AM2=122−52=119cm
⇒SO=√SM2−OM2=√119−52=√94cm⇒SO=SM2−OM2=119−52=94cm
⇒VS.ABCD=13.SABCD.SO=13.AB2.SO=102.943=94003cm3
Chọn đáp án A
Gọi O là giao điểm của AC và BD.
Áp dụng định lí Pytago vào tam giác vuông ABC có:
Áp dụng định lí Pytago vào tam giác vuông SAO có:
S O 2 = S A 2 - A O 2 = 13 2 - 5 2 = 144 nên SO = 12cm