Cho hình chóp S.ABC có ABC là tam giác đều cạnh a và SA vuông góc với đáy. Góc tạo bởi SB và mặt phẳng (ABC) bằng 60 o . Tính khoảng cách từ A đến mặt phẳng (SBC)
A. a 15 5
B. a 15 3
C. 3 a 5
D. 5 a 3
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

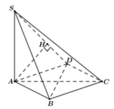
Xác định được ![]()
Khi đó ta tính được ![]()
Trong mặt phẳng (ABC) lấy điểm D sao cho ABCD là hình chữ nhật
=> AB//CD nên
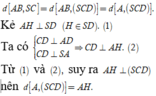
Xét tam giác vuông SAD có 
Chọn C.

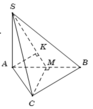
Xác định được 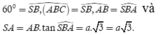
Do M là trung điểm của cạnh AB nên ![]()
![]()
Tam giác vuông SAM, có 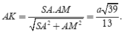
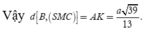
Chọn B.

Đáp án A
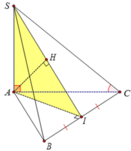
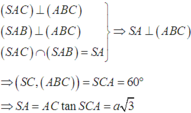
Gọi I,H lần lượt là hình chiếu vuông góc của A trên BC, SI, khi đó: d(A, (SBC)) =AH
Tam giác ABC đều cạnh a nên AI = a 3 2
Khi đó xét tam giác SAI :
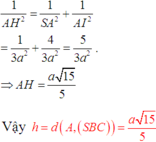

Đáp án C
Phương pháp:
- Xác định góc giữa hai mặt phẳng S.ABC bởi định nghĩa:
Góc giữa hai mặt phẳng là góc giữa hai đường thẳng nằm trong hai mặt phẳng mà cùng vuông góc với giao tuyến.
- Tính thể tích khối chóp theo công thức
V = 1 3 S h
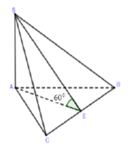


Chọn A
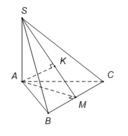
Gọi M là trung điểm BC
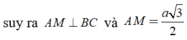
Gọi K là hình chiếu của A trên SM , suy ra AK ⊥ SM. (1)
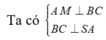
![]()
![]()
![]()
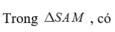
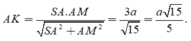
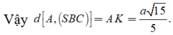
Kẻ A H ⊥ B C và A H ⊥ S I . Khi đó A H ⊥ S B C ⇒ d A , S B C = A H
Ta có A I = a 3 2 (do ∆ A B C đều cạnh a)
và
S B A B C = S B A ^ = 60 o ⇒ S A = A B . tan 60 = a 3
Vậy d A S B C = A H = S A . A I S A 2 + A I 2 = a 15 5
Đáp án A