Cho tam giác ABC thỏa mãn: sinC = cosA + cosB. Tìm mệnh đề đúng
A. Tam giác ABC cân tại A
B. Tam giác ABC là tam giác nhọn
C. Tam giác ABC đều
D. Tam giác ABC là tam giác vuông.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
15 tháng 2 2019
Đáp án: D
a sai vì nếu tam giác ABC thỏa mãn AB2 + AC2 = BC2 thì tam giác ABC vuông tại A không phải vuông tại B.
b, c, d đúng.
CM
14 tháng 1 2017
a) Nếu ABC là một tam giác cân thì ABC là tam giác đều
Đây là mệnh đề sai
b) Nếu ABC là một tam giác cân và có một góc bằng 60o thì ABC là một tam giác đều
Đây là mệnh đề đúng
24 tháng 10 2016
Giả thiết của dề bài chưa đúng, mình sửa lại thành \(cosA+cosB+cosC=\sqrt{cosA.cosB}+\sqrt{cosB.cosC}+\sqrt{cosC.cosA}\)
Đặt \(a=\sqrt{cosA},b=\sqrt{cosB},c=\sqrt{cosC}\)
Suy từ giả thiết :
\(2\left(a^2+b^2+c^2\right)=2\left(ab+bc+ca\right)\)
\(\Leftrightarrow\left(a-b\right)^2+\left(b-c\right)^2+\left(c-a\right)^2=0\)
\(\Leftrightarrow\hept{\begin{cases}a=b=c\\a,b,c>0\end{cases}}\)
Vậy ta có \(\sqrt{cosA}=\sqrt{cosB}=\sqrt{cosC}\Rightarrow\hept{\begin{cases}cosA=cosB=cosC\\\widehat{A}+\widehat{B}+\widehat{C}=180^o\end{cases}}\)
\(\Rightarrow\widehat{A}=\widehat{B}=\widehat{C}=60^o\)
\(\Rightarrow\Delta ABC\) là tam giác đều.
HQ
Hà Quang Minh
Giáo viên
1 tháng 10 2023
a)
\(P \Rightarrow Q\): “Nếu tam giác ABC là tam giác vuông tại A thì các cạnh của nó thỏa mãn \(A{B^2} + A{C^2} = B{C^2}\)”
Mệnh đề này đúng.
\(Q \Rightarrow P\): “Nếu tam giác ABC có các cạnh thỏa mãn \(A{B^2} + A{C^2} = B{C^2}\) thì tam giác ABC vuông tại A”
Mệnh đề này đúng.
\(P \Leftrightarrow Q\): “Tam giác ABC là tam giác vuông tại A khi và chỉ khi các cạnh của nó thỏa mãn \(A{B^2} + A{C^2} = B{C^2}\)”
Mệnh đề này đúng do các mệnh đề \(P \Rightarrow Q,Q \Rightarrow P\)đều đúng.
\(\overline P \Rightarrow \overline Q \): “Nếu tam giác ABC không là tam giác vuông tại A thì các cạnh của nó thỏa mãn \(A{B^2} + A{C^2} \ne B{C^2}\)”
Mệnh đề này đúng.
b) Mệnh đề \(P \Rightarrow Q\) có thể phát biểu là:
“Tam giác ABC là tam giác vuông tại A là điều kiện đủ để tam giác ABC có các cạnh thỏa mãn \(A{B^2} + A{C^2} = B{C^2}\)”
“Tam giác ABC có các cạnh thỏa mãn \(A{B^2} + A{C^2} = B{C^2}\) là điều kiện cần để tam giác ABC vuông tại A”
c)
X là tập hợp các tam giác ABC vuông tại A.
Y là tập hợp các tam giác ABC có trung tuyến \(AM = \frac{1}{2}BC\).
Dễ thấy: \(X \subset Y\) do các tam giác ABC vuông thì đều có trung tuyến \(AM = \frac{1}{2}BC\).
Ta chứng minh: Nếu tam giác ABC có trung tuyến \(AM = \frac{1}{2}BC\) thì tam giác ABC vuông tại A.
Thật vậy, \(BM = MC = AM = \frac{1}{2}BC\) suy ra M là tâm đường tròn đường kính BC, ngoại tiếp tam giác ABC.
\( \Rightarrow \widehat {BAC} = {90^ \circ }\) (góc nội tiếp chắn nửa đường tròn)
Vậy tam giác ABC là tam giác vuông.
Do đó \(Y \subset X\)
Vậy \(X = Y\)
Chọn D.
Ta có:
Vậy sin C = cosA + cos B khi và chỉ khi
Hay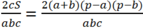
Nên c2[(a + b) 2 - c2]= (a + b)2[ c2 - (a - b)2]
Do đó; c4 = (a2 - b2) 2
Suy ra a2 = b2 + c2 hoặc b2 = c2 + a2
Suy ra; tam giác ABC vuông tại A hoặc B.