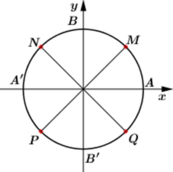
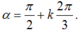Biết OMB’ và ONB’ là các tam giác đều. Cung α có mút đầu là A và mút cuối là B hoặc M hoặc N. Tính số đo của α?
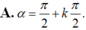
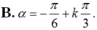
![]()
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn D.
+ Cung α có mút đầu là A và mút cuối là M theo chiều dương có số đo là ![]() nên loại A,C.
nên loại A,C.
+ Cung α có mút đầu là A và mút cuối là M theo chiều âm có số đo là ![]() và chỉ có duy nhất một điểm M trên đường tròn lượng giác nên loại B.
và chỉ có duy nhất một điểm M trên đường tròn lượng giác nên loại B.

Chọn A.

+ Vì L là điểm chính giữa 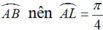
+ Vì N là điểm chính giữa 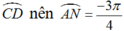
+ Ta có 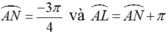
Vậy L hoặc N là mút cuối của 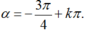

Chọn D.
+ Ta có số đo cung ![]()
+ Ta có ![]()
+ Để mút cuối cùng trùng với một trong bốn điểm M; N; P; Q thì chu kì của cung α là ![]()
Vậy số đo cung ![]()

a: BM là phân giác của góc ABC
=>\(\widehat{ABM}=\widehat{MBC}=\dfrac{\widehat{ABC}}{2}\)
CM là phân giác của góc ACB
=>\(\widehat{ACM}=\widehat{MCB}=\dfrac{\widehat{ACB}}{2}\)
Xét ΔMBC có \(\widehat{MBC}+\widehat{MCB}+\widehat{BMC}=180^0\)
=>\(\widehat{BMC}+\dfrac{\widehat{ABC}+\widehat{ACB}}{2}=180^0\)
=>\(\widehat{BMC}+\dfrac{180^0-\widehat{BAC}}{2}=180^0\)
=>\(\widehat{BMC}+\dfrac{180^0-a}{2}=180^0\)
=>\(\widehat{BMC}=180^0-90^0+\dfrac{a}{2}=\dfrac{a}{2}+90^0\)
Vì BM,BN lần lượt là phân giác trong và phân giác ngoài tại đỉnh B của ΔABC nên BM\(\perp\)BN
=>\(\widehat{MBN}=90^0\)
Vì CM,CN lần lượt là phân giác trong và phân giác ngoài tại đỉnh C của ΔABC nên CM\(\perp\)CN
=>\(\widehat{MCN}=90^0\)
Xét tứ giác BMCN có \(\widehat{BMC}+\widehat{BNC}+\widehat{MBN}+\widehat{MCN}=360^0\)
=>\(\widehat{BNC}+90^0+\dfrac{a}{2}+90^0+90^0=360^0\)
=>\(\widehat{BNC}=90^0-\dfrac{a}{2}\)
b: Xét tứ giác BMCN có \(\widehat{MBN}+\widehat{MCN}=90^0+90^0=180^0\)
nên BMCN là tứ giác nội tiếp đường tròn đường kính MN
=>B,M,C,N cùng thuộc đường tròn tâm O đường kính MN
Tâm O là trung điểm của MN
Chọn C.
+ Cung α có mút đầu là A và mút cuối là B nên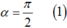
OMB’và ONB’ là các tam giác đều nên
+ Cung α có mút đầu là A và mút cuối là M hoặc N nên
+ Chu kì của cung α là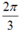
Từ (1), (2) ta có