Trong mặt phẳng với hệ tọa độ Oxy cho ba điểm A(0;a) : B( b;0) và C(-b;0) với a; b > 0.Viết phương trình đường tròn (C) tiếp xúc với đường thẳng AB tại B và tiếp xúc với đường thẳng AC tại C.
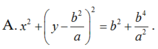
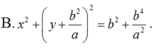
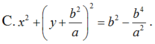
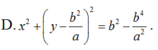
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn C.
Phương pháp:
Viết phương trình đường thẳng dưới dạng phương trình đoạn chắn.
Cách giải:
![]()

Lời giải:
Tọa độ trung điểm $M$ của $AB$ là:
\(\left(\frac{x_A+x_B}{2}; \frac{y_A+y_B}{2}\right)=\left(\frac{2+0}{2}; \frac{5+(-7)}{2}\right)=(1;-1)\)

\(\overrightarrow{AB}=\left(x_B-x_A;y_B-y_A\right)=\left(3;-9\right)\)

Chọn C.
Phương pháp: Dựa vào dữ kiện bài toán để xác định tọa độ điểm M.
Cách giải: Ta có:


Đáp án C
Áp dụng STUDY TIPS bên, ta có:
Khoảng cách từ điểm M đến mặt phẳng O x y là a=2.
Khoảng cách từ điểm M đến mặt phẳng O x y là b=1.
Khoảng cách từ điểm M đến mặt phẳng O x y là c=3 .
Vậy P = a + b 2 + c 3 = 2 + 1 2 + 3 3 = 30 .

Đáp án C
Gọi I(x;y;0) là tâm của mặt cầu (S) ⇒ A I → = x - 1 ; y - 2 ; 4 A I → = x - 1 ; y + 3 ; - 1 A I → = x - 2 ; y - 2 ; - 3
Theo bài ra, ta có
I A = I B I A = I C ⇒ x - 1 2 + y - 2 2 + 4 2 = x - 1 2 + y + 3 2 + - 1 2 x - 1 2 + y - 2 2 + 4 2 = x - 2 2 + y - 2 2 + - 3 2 ⇔ x = - 2 y = 1
Vậy I ( - 2 ; 1 ; 0 ) ⇒ A I → = ( - 3 ; - 1 ; 4 ) ⇒ l = 2 . I A = 2 16 .

Chọn C
Gọi tâm mặt cầu là: I(x;y;0).
I A = I B I A = I C ⇔ ( x - 1 ) 2 + ( y - 2 ) 2 + 4 2 = ( x - 1 ) 2 + ( y + 3 ) + 1 2 ( x - 1 ) 2 + ( y - 2 ) 2 + 4 2 = ( x - 2 ) 2 + ( y - 2 ) 2 + 3 2 ⇔ ( y - 2 ) 2 + 4 2 = ( y + 3 ) 2 + 1 2 x 2 - 2 x + 1 + 16 = x 2 - 4 x + 4 + 9 ⇔ 10 y = 10 2 x = - 4 ⇔ x = - 2 y = 1 ⇒ i = 2 R = 2 ( - 3 ) 2 + ( - 1 ) 2 + 4 2 = 2 26
Đáp án B
Do đường tròn (C) tiếp xúc với đường thẳng AB tại B và tiếp xúc với đường thẳng AC tại C
Nên tam giác ABC cân tại A
tâm I của (C) thuộc Oy nên I(0; y0)
Do:
Mặc khác:
Vậy phương trình của là: