Cho d : x = 2 + 2 t y = 3 + t ( t ∈ ℝ ) Tìm điểm M trên d cách A(0;1) một đoạn bằng 5
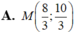
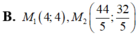
![]()
D. M( 2; -3)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án D.
Hai đường thẳng d và d ' cắt nhau khi và chỉ khi hệ phương trình
1 + a 2 t = 3 − t ' t = 2 + t ' − 1 + 2 t = 3 − t ' có đúng một nghiệm ⇔ t = 2 t ' = 0 a = ± 1 .
Vậy ta chọn D.

Thay tọa độ (5 ;3) vào phương trình tham số:
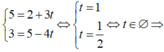
không có t nào thỏa mãn.
Chọn A.

Do A nằm trên d nên thay tọa độ điểm A vào phương trình tham số đường thẳng d:
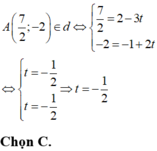

Đáp án B
Ta có:
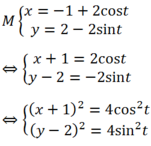
=> ( x +1) 2+ (y- 2) 2= 4cos2t + 4sin2t
=> ( x +1) 2+ (y- 2) 2 = 4
Vậy tập hợp điểm M là phương trình đường tròn có tâm I( -1;2) , bán kính R= 2.

Đáp án: A

Vì d vuông góc với d’ nên d sẽ nhận vecto chỉ phương của d’ làm vecto pháp tuyến
Vậy d là đường thẳng đi qua M và có vecto pháp tuyến là 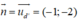
d: -1(x - 2) - 2(y + 3) = 0 ⇔ -x - 2y - 4 ⇔ x + 2y + 4 = 0

Chọn B

Vậy M(3;−4;−2) là giao điểm của đường thẳng d và mặt phẳng (P).
Lấy điểm M( 2+ 2t; 3+ t) nằm trên d;
Để AM= 5 khi và chỉ khi
(2t+2) 2+ (t+2) 2= 25 hay 5t2+12t- 17= 0
Suy ra t= 1 hoặc t= - 17/5
Với t= 1 thì M( 4;4)
Chọn C.