Cho đa thức:
P ( x ) = ( 1 + x ) + 2 ( 1 + x ) 2 + 3 ( 1 + x ) 3 + . . .
+ 20 ( 1 + x ) 20
Được viết dưới dạng
P ( x ) = a 0 + a 1 x + a 2 x 2 + . . . + a 20 x 20 .
Tìm hệ số của a15?
A. 400995
B. 500995
C. 600995
D. 700995
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

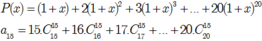


Bài 1.
x^3 + 3x^2 + 3 x^3 + 1 1 1 x^3 - 3x^2 + 2
3x2 + 2 có bậc thấp hơn x3 + 1 nên không thể chia tiếp
Vậy x3 + 3x2 + 3 = 1( x3 + 1 ) + 3x2 + 2
Bài 2.
Ta có : x3 + 3x2 + 3x + a có bậc là 3
x + 2 có bậc là 1
=> Thương bậc 2
lại có hệ số cao nhất của đa thức bị chia là 1
Đặt đa thức thương là x2 + bx + c
khi đó : x3 + 3x2 + 3x + a chia hết cho x + 2
<=> x3 + 3x2 + 3x + a = ( x + 2 )( x2 + bx + c )
<=> x3 + 3x2 + 3x + a = x3 + bx2 + cx + 2x2 + 2bx + 2c
<=> x3 + 3x2 + 3x + a = x3 + ( b + 2 )x2 + ( c + 2b )x + 2c
Đồng nhất hệ số ta được :
\(\hept{\begin{cases}b+2=3\\c+2b=3\\2c=a\end{cases}}\Leftrightarrow\hept{\begin{cases}b=1\\c=1\\a=2\end{cases}}\Rightarrow a=2\)
Vậy a = 2

Bài 1 : Đa thức chia là bậc 2 do đó đa thức dư nhiều nhất sẽ là bậc 1 .
Ta có : \(P\left(x\right)=Q\left(x\right).\left(x^2-5x+6\right)+ax+b\)
Theo bài ra ta có hệ phương trình :
\(\left\{{}\begin{matrix}P\left(2\right)=2a+b=-2\\P\left(3\right)=3a+b=-3\end{matrix}\right.\)
Giải hệ phương trình ta tìm được :
\(\left\{{}\begin{matrix}a=-1\\b=0\end{matrix}\right.\)
Vậy số dư trong phéo chia là \(-x\)
Bài 2 : Mình suy nghĩ sau !
Chúc bạn học tốt

Gọi thương của P(x) khi chi cho (x-2), (x-3) lần lượt là A(x),B(x) =>P(x)=(x-2).A(x)+5 (1) và P(x)=(x-3).B(x)=7 (2) Gọi thương của P(x) khi chia cho (x-2).(x-3) là C(x) và dư là R(x) Ta có : (x-2)(x-3) có bậc là 2 => R(x) có bậc là 1 => R(x) có dạng ax+b (a,b là số nguyên ) =>R(x)=(x-2)(x-3).C(x)+ax+b (3) thay x=2 vào (1) và (3) ta có: P(x)=2a+b=5 thay x=3 vào (2) và (3) ta có: P(x)=3a+b=7 => a=2,b=1 =>R(x)=2x+1 Vậy dư của P(x) khi chia cho (x-2)(x-3) là 2x+1

1: f(-1)=0
=>1+m-1+3m-2=0 và
=>4m-2=0
=>m=1/2
2: g(2)=0
=>2^2-4(m+1)-5m+1=0
=>4-5m+1-4m-4=0
=>-9m+1=0
=>m=1/9
4: f(1)=g(2)
=>1-(m-1)+3m-2=4-4(m+1)-5m+1
=>1-m+1+3m-2=4-4m-4-5m+1
=>2m-2=-9m+1
=>11m=3
=>m=3/11
3:
H(-1)=0
=>-2-m-7m+3=0
=>-8m=-1
=>m=1/8
5: g(1)=h(-2)
=>1-2(m+1)-5m+1=-8-2m-7m+3
=>-5m+2-2m-2=-9m-5
=>-7m=-9m-5
=>2m=-5
=>m=-5/2