Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
b) Xét tứ giác A’BCD’ có BC//A’D’ và BC = A’D’
=> tứ giác A’BCD’ là hình bình hành
=> BA’ // CD’ ( tính chất của hình bình hành)
Tương tự, tứ giác ABC’D’ là hình bình hành nên BC’//AD’
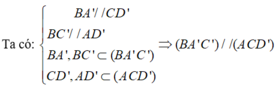
Gọi O và O’ là tâm của ABCD và A’B’C’D’.
Gọi H và I lần lượt là tâm của hai tam giác đều BA’C’ và ACD’.
* Xét ( BB’D’D) có BO’// D’O nên OI // HB
Lại có: O là trung điểm BD
=> I là trung điểm của HD: IH = ID (1)
* Xét (BB’D’D) có D’O// BO’ nên D’I // HO’
Lại có: O’ là trung điểm của B’D’ nên H là trung điểm B’I: HI = HB’ (2)
Từ (1) và (2) suy ra: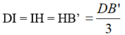 
* Theo phần trên B'D ⊥ (BA'C) ⇒ IH ⊥ (BA'C)
Mà I ∈ (ACD') nên khoảng cách giữa hai mp song song (ACD’) và ( BA’C’) là độ dài đoạn IH.
Khi đó:
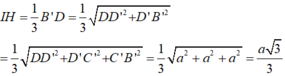
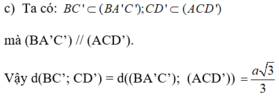
Đáp án A.
Vẽ DH ⊥ A'C
Ta có: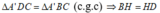
Vậy góc giữa hai mặt phẳng (BA'C) và (DA'C) là góc B H D ^
Trong ∆ A'DC vuông tại D
Trong ∆ HBD có
Suy ra góc giữa hai mặt phẳng (BA'C) và (DA'C) là góc 60°.