Cho hình chóp S.ABCD có đáy ABCD là hình thoi tâm O. Biết SA = SC và SB = SD. Chứng minh: SO ⊥ AB.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
16 tháng 2 2021
bị thừa nha bn tham khảo bn cần thì chép đến phần A thôi nha!
HQ
Hà Quang Minh
Giáo viên
22 tháng 9 2023
+) Xét tam giác SAC có SA = SC \( \Rightarrow \) SAC là tam giác cân mà SO là trung tuyến
\( \Rightarrow \) SO \( \bot \) AC.
Xét tam giác SBD có SB = SD \( \Rightarrow \) SBD là tam giác cân mà SO là trung tuyến
\( \Rightarrow \) SO \( \bot \) BD.
+) Ta có SO \( \bot \) AC; SO \( \bot \) BD; AC \( \cap \) BD tại O \( \Rightarrow \) SO \( \bot \) (ABCD).
CM
12 tháng 2 2017
Đáp án B
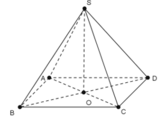
+) Tam giác SAC cân tại S có SO là trung tuyến
⇒ SO cũng là đường cao ⇒ SO ⊥ AC.
+) Tam giác SBD cân tại S có SO là trung tuyến
⇒ SO cũng là đường cao ⇒ SO ⊥ BD.
- Từ đó suy ra SO ⊥ (ABCD).
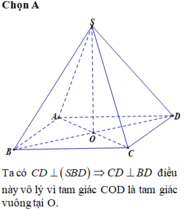
→ Do ABCD là hình thoi nên CD không vuông góc với BD. Do đó CD không vuông góc với (SBD).
25 tháng 4 2023
1: BC vuông góc AB
BC vuông góc SA
=>BC vuông góc (SAB)
=>(SAB) vuông góc (SBC)
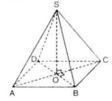
- Hình thoi ABCD có tâm O nên O là trung điểm AC và BD.
+) Tam giác SAC cân tại S( vì SA = SC) có SO là trung tuyến.
⇒ SO cũng là đường cao ⇒ SO ⊥ AC (1)
+) Tam giác SBD cân tại S( vì SB = SD) có SO là trung tuyến
⇒ SO cũng là đường cao ⇒ SO ⊥ BD (2)
- Từ (1), (2) suy ra S) ⊥ (ABCD).
+) Lại có: AB ⊂ mp(ABCD) nên SO ⊥ AB.