Tìm điều kiện của tham số m để phương trình
cos 2 x - 4 cos x + m = 0 có nghiệm.
![]()
![]()
![]()
![]()
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C
Sử dụng tính đơn điệu của hàm số, đánh giá số nghiệm của phương trình.
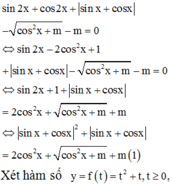
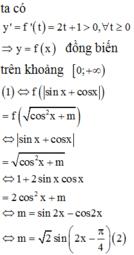

Vậy, có 3 giá trị nguyên của m thỏa mãn yêu cầu đề bài.

Đáp án C
Ta có : PT <=> log2 |cos x| – 2mlog|cos x| – m2 + 4 = 0
Đặt t = log|cos x|; t ∈ ( - ∞ ; 0 ]
Khi đó: t2 – 2mt – m2 + 4 = 0 (*)
PT đã cho vô nghiệm <= > (*) vô nghiệm hoặc có nghiệm dương.


Phương trình mx2 – 2(m – 1)x + m − 3 = 0
(a = m; b = −2(m – 1); c = m – 3)
TH1: m = 0 ta có phương trình
2x – 3 = 0 ⇔ 2x = 3 ⇔ x = 3 2
TH2: m ≠ 0, ta có ∆ = b2 – 4ac = 4 (m – 1)2 – 4m. (m – 3)
= 4m2 – 8m + 4 – 4m2 + 12 = 4m + 4
Để phương trình đã cho có nghiệm thì ∆ ≥ 0
⇔ 4m + 4 ≥ 0 ⇔ 4m ≥ −4 ⇔ m ≥ −1
Vậy để phương trình đã cho có nghiệm thì m ≥ −1
Đáp án cần chọn là: C

Phương trình mx2 + 2(m + 1)x + 1 = 0 (a = m; b = 2 (m + 1); c = 1)
TH1: m = 0 ta có phương trình 2x + 1 = 0
⇔ x = − 1 2 nên nhận m = 0 (1)
TH2: m ≠ 0, ta có = 4(m + 1)2 – 4m.1 = 4m2 + 4m + 4
= 4m2 + 4m + 1 + 3= (2m + 1)2 + 3
Để phương trình đã cho có nghiệm thì
∆ ≥ 0 ⇔ (2m + 1)2 + 3 ≥ 0
⇔ (2m + 1)2 ≥ −3 (luôn đúng với mọi m) (2)
Từ (1) và (92) ta thấy phương trình đã cho có nghiệm với mọi m ∈ ℝ
Đáp án cần chọn là: D

\(x^2+\left(4m+1\right)x+2\left(m-4\right)=0\)
\(\Delta=\left(4m+1\right)^2-4\cdot1\cdot2\left(m-4\right)=16m^2+8m+1-8m+32=16m^2+33\ge33>0\forall m\)
\(\Leftrightarrow\left\{{}\begin{matrix}x_1=\dfrac{-\left(4m+1\right)+\sqrt{16m^2+33}}{2}\\x_2=\dfrac{-\left(4m+1\right)-\sqrt{16m^2+33}}{2}\end{matrix}\right.\)
Mà: \(x_2-x_1=17\)
\(\Leftrightarrow\dfrac{-\left(4m+1\right)-\sqrt{16m^2+33}}{2}-\dfrac{-\left(4m+1\right)+\sqrt{16m^2+33}}{2}=17\)
\(\Leftrightarrow\dfrac{-\left(4m+1\right)-\sqrt{16m^2+33}+\left(4m+1\right)-\sqrt{16m^2+33}}{2}=17\)
\(\Leftrightarrow\dfrac{-2\sqrt{16m^2+33}}{2}=17\)
\(\Leftrightarrow\sqrt{16m^2+33}=-17< 0\)
Vậy không có m thỏa mãn
Đáp án D