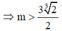Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Đáp án B
Áp dụng công thức giải nhanh
S = b 4 a 2 − b 2 a = 4 4 2 2 = 1.
Chú ý công thức tính nhanh dạng này là:
S = b 2 4 a − b 2 a và tan 2 A 2 = − 8 a b 3 .
Đáp án A
PT hoành độ giao điểm:
x 3 + x 2 + m = 0 ⇔ − m = x 3 + x 2 = f x
Xét hàm số: f x = x 3 + x 2 ⇒ f ' x = 3 x 2 + 2 x = 0
⇔ x = 0 ⇒ y = 0 x = − 2 3 ⇒ y = 4 27
Lập BBT hoặc vẽ đồ thị suy ra PT có đúng nghiệm
⇔ − m < 0 − m > 4 27 ⇒ m > 0 m < − 4 27 .
Đáp án A
y ' = 4 x 3 − 2 mx
Để đồ thị cắt trục hoành tại 4 điểm phân biệt thì đồ thị hàm số phải có 3 cực trị và y C T < 0 < yCĐ Nên m>0 và y’=0 có 3 nghiệm
y ' = 0 ⇔ x= 0 x= 2 m 2 x=- 2 m 2
y C T < 0 < yCĐ ⇔ − m 2 4 + m − 1 < 0 < m − 1 ⇔ 2 ≠ m > 1
Đáp án A
y ' = 4 x 3 − 2 mx
Để đồ thị cắt trục hoành tại 4 điểm phân biệt thì đồ thị hàm số phải có 3 cực trị và y C T < 0 < yCĐ Nên m > 0 và y’=0 có 3 nghiệm
y ' = 0 ⇔ x= 0 x= 2 m 2 x=- 2 m 2
y C T < 0 < y C Đ ⇔ − m 2 4 + m − 1 < 0 < m − 1 ⇔ 2 ≠ m > 1
Đáp án B
Phương pháp:
+) Xác định m để phương trình hoành độ giao điểm có 3 nghiệm phân biệt.
+) Cô lập m, sử dụng phương pháp hàm số.
Cách giải:
Phương trình hoành độ giao điểm của đồ thị hàm số y = x3 - mx + 1 và trục hoành là: x3 - mx + 1 = 0
⇔ x3 - mx + 1 = 0 ⇔ mx = x3 + 1(*)
+) x = 0:(*) ⇔ m.0 = 1: vô lý Phương trình (*) không có nghiệm x = 0 với mọi m
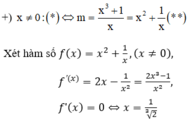
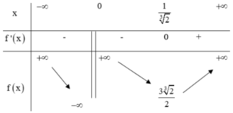
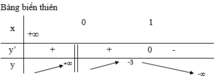
Số nghiệm của phương trình (**) là số giao điểm của đồ thị hàm số 
và đường thẳng y = m song song với trục hoành.
Để phương trình ban đầu có 3 nghiệm phân biệt ⇔ (**) có 3 nghiệm phân biệt khác 0
và 
và 