Một hình vuông ABCD có cạnh AB = x, diện tích S1. Nối bốn trung điểm A1, B1, C1, D1 theo thứ tự của 4 cạnh AB, BC, CD, DA ta được hình vuông thứ hai A1B1C1D1 có diện tích S2. Tiếp tục như thế ta được hình vuông thứ ba A2B2C2D2 có diện tích S3 và cứ tiếp tục như thế ta được diện tích thứ S4, S5,…Tìm x để S 1 + S 2 + S 3 + . . . + S 100 = 2 100 - 1 2 99
![]()
![]()
![]()
![]()



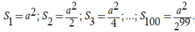
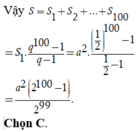
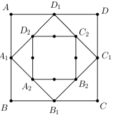
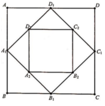



Chọn B